
我一直都很佩服那些可以直接用LATEX语法打出各种复杂数学公式的人,反正我是记不住,而且也真的不想去记LATEX语法。
比如这个公式:
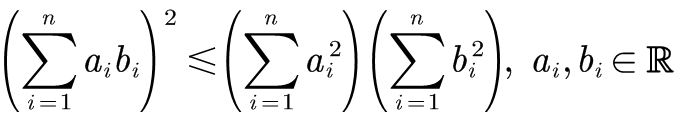
有的人能直接用LATEX手写出来:
\left( \sum_{i=1}^n{a_ib_i} \right) ^2\leqslant \left( \sum_{i=1}^n{a_{i}^{2}} \right) \left( \sum_{i=1}^n{b_{i}^{2}} \right) , a_i,b_i\in \mathbb{R}
这还算简单的了,更复杂的公式大神们都可以直接手写LATEX。
就问你服不服。
在下自愧脑容量不足。
所以当我要输入数学公式的时候,MathType这个功能强大的可视化数学公式编辑器就是我认为最方便易用的软件。






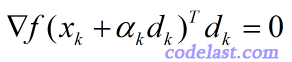


![y = \sqrt[3]{x},y = \sqrt {{x^2}} = \left| x \right|](https://www.codelast.com/wp-content/plugins/latex/cache/tex_9b4fbea1e8a995125a014c281dedeac9.gif)
