在一台服务器上，如果启动了一个TF-Serving服务，我们知道它占了资源，却不知道它是在空跑还是真的在用。
本文描述了怎样判断它是否真的在用。
Algorithm
[原创]《使用 fastText 做中文文本分类》文章合集
本文描述了如何使用 fastText 对中文进行文本分类的过程，只有实操，基本没有理论。
以下按顺序编排。
✓ 使用 fastText 做中文文本分类(1)
✓ 使用 fastText 做中文文本分类(2)
✓ 使用 fastText 做中文文本分类(3)
✓ 使用 fastText 做中文文本分类(4)
✓ 使用 fastText 做中文文本分类(5)… Read More
[原创] 使用 fastText 做中文文本分类(4)
查看本系列文章合集，请看这里。
✓ 开始训练第一个文本分类模型
标注好的数据，其格式为：
__label__科技 月 10 日 网通 社从 高合 汽车 获悉 华人 运通 微软 2020 世界 人工智能 大会 云端 峰会 WAIC 2020 上 达成 战略 合作 依托 微软 小冰 人工智能 技术 高合 汽车 上 落地 全球 首个 主动式 人工智能 伙伴 HiPhiGo 用户 提供 更好 交通 出行 体验 人工智能 交通 行业 创新 融合 发展 探讨 成立 联合 智能 计算 实验室 智能 汽车 载体 智捷 交通 多个 领域 展开 深度 合作 人工智能 前瞻 技术 研发 推动 智慧 出行 社会 持续 发展 微软 亚洲 互联网 工程院 院长 王永东 微软 华人 运通 合作 使 人工智能 技术 切实可行 落地 场景 得以 转化 真实有效 生产力 发挥 更大 价值 微软 华人 运通 携手 推进 人工智能 新兴 科技 汽车 智慧 智慧 出行 领域 广泛应用 产业 升级 社会 持续 发展 注入 新 活力 华人 运通 董事长 丁磊 此次 合作 顶级 人工智能 企业 智能 汽车 公司 强强 联手 AI 多项 领先 技术 全球 汽车行业 首次 量产 落地 世界 内 技术 领先 性 首款 智能 汽车 高合 HiPhi 有条不紊 推进 全球 首条 车路 协同 自动 驾驶 智能化 城市道路 示范 项目 盐城 开通 试运行 再 全球 首个 车路 城 一体化 5G 无人驾驶 交通 运营 样板 上海 张江 未来 公园 成功 落地 华人 运通 以人为本 人性化 需求 出发 人性化 智慧 打造 智能 汽车 智捷 交通 智慧 城市 三智 战略 各项 业务 稳步 推进 高合 首款 量产 车 HiPhi 2020 年底 小批量 试生产 2021 年 上市 交付
按 fastText 的指南，把这份数据按大概 9:1 的比例，分成training集和validation集，然后开始训练模型：
./fasttext supervised -input labeled-data_train -output model
其中，labeled-data_train 是training集文件，model 是输出模型的文件名前缀。
经过一段时间的等待（速度很快），当前目录下就生成了模型文件：model.bin 和 model.vec。
[原创] 使用 fastText 做中文文本分类(3)
查看本系列文章合集，请看这里。
为 training 数据做标注，这可能是一个艰巨的任务，也可能是一个有捷径的任务。
有时候，我们可以依据一些已知的规则来标注文本，比如不同的数据是从不同的来源获取到的，从来源可以知道它们所属的类别，这是一个捷径。不过我这里不具备这样的条件。
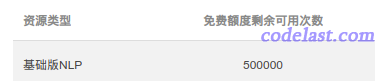
我的数据来源是网上的各种新闻，不是某些专业领域的数据，这种比较常见的文本分类任务，可以利用国内的几大云服务商提供的免费接口来完成。阿里云、腾讯云都有这样的接口。
以腾讯云为例，其“人工智能→自然语言处理”产品提供了文本分类功能：
文本分类接口能够对用户输入的文本进行自动分类，将其映射到具体的类目上，用户只需要提供待分类的文本，而无需关注具体实现。该功能基于千亿级大规模互联网语料和LSTM、BERT等深度神经网络模型进行训练，并持续迭代更新，以保证效果不断提升。目前已提供：● 通用领域分类体系，包括15个分类类目，分别是汽车、科技、健康、体育、旅行、教育、职业、文化、军事、房产、娱乐、女性、奥运、财经以及其他，适用于通用的场景。● 新闻领域分类体系，包括37个一级分类类目，285个二级分类（详细请见 类目体系映射表），已应用于腾讯新闻的文章分类。更多垂直领域的分类体系即将推出，敬请期待。默认接口请求频率限制：20次/秒。
该API每天有50万次免费调用额度，用来标注数据够用了：
如果你对这个接口的分类结果准确性有疑虑的话，可以亲自拿一些新闻的文本试一试，就会发现它的效果真的不错，完全可以用来当作人工标注的结果了，毕竟是大厂出品嘛。
如果你对这个接口的分类结果准确性有疑虑的话，可以亲自拿一些新闻的文本试一试，就会发现它的效果真的不错，完全可以用来当作人工标注的结果了，毕竟是大厂出品嘛。
[原创] 使用 fastText 做中文文本分类(2)
查看本系列文章合集，请看这里。
做好文本预处理，才能输入fastText训练一个效果好的模型出来。
✓ 原文示例
有时我们拿到的源数据是很粗糙的，带有很多会影响模型效果的内容，例如下面这样：
<p>罗望子，是豆科酸豆属唯一的种，是热带乔木，原产于东部非洲，包括马达加斯加落叶森林，但已被引入热带亚洲、拉丁美洲和加勒比海。柽柳是中国海南省三亚的一种城市树木。罗望子最适合生长在温度高、日照长、气候干燥、干湿季节分明的地区。</p><p><img src="http://p0.qhimg.com/t014b83dc78c7cc5000.jpg?size=741x320"/><br /></p><p>罗望子富含糖、乙酸、酒石酸、甲酸、柠檬酸等成分，主要用于调味品、饮料、果酱等食品领域。吃一点罗望子有很多好处。当我们吃罗望子时，罗望子中含有的多糖是一种非常好的抗光物质。当我们吃这种物质时，它可以防止紫外线辐射伤害皮肤。通常吃一点罗望子，饭前吃一点罗望子可以增进食欲，改善我们的饮食质量。在炎热的夏日，吃一点罗望子可以生津止渴，清热解毒，降低中暑的风险。</p><p><img src="http://p1.qhimg.com/t01ecdbbc26c329a78b.jpg?size=533x409"/><br /></p><p>罗望子种子含有丰富的抗氧化物质。多吃罗望子籽可以延缓人体衰老，保持皮肤湿润有光泽。罗望子种子还含有一些清热解毒、消炎的物质，可以帮助我们的人体抵抗一些有害细菌，保护我们的健康。
这里面不仅带有URL、大量的HTML标签，而且还有标点符号等，这些都要清洗掉。
[原创] 使用 fastText 做中文文本分类(1)
查看本系列文章合集，请看这里。
✓ 什么是“文本分类”
它是图书馆学， 信息学和计算机科学中的一个问题。其任务是将一个文档分配到一个或者多个类别中。
举例：
| 文本 | 类别 |
| 瑞幸咖啡今日发布声明称，瑞幸咖啡公司将于6月29日在纳斯达克停牌，并进行退市备案。声明表示，在国内消费市场方面，瑞幸咖啡全国4000多家门店将正常运营，近3万名员工仍将一如既往的为用户提供优质产品和服务。公司衷心感谢广大消费者的支持厚爱，并再次为事件造成的恶劣影响向社会各界诚挚道歉。 | 财经 |
| 明朝中后期西南沿海一个重要的问题就是倭寇的骚扰，这个问题本来是有希望被当时的浙江总督用和平的方法解决掉的，但是中途就出了个王本固这个插曲。 | 历史 |
其中，“类别”是事先定义好的。一段文本可以属于多个类别，例如，第2个例子可以同时属于“历史”和“明朝”这两个类别。
[原创] 调戏了一番度娘"最先进"的PLATO-2预训练模型之后，我还是回到了和人类交谈...
（莫慌，这图是拿出来撑场面的，我可能和你一样看不懂）
前言：这是一篇很不严肃的实验文章。每一个会修电脑的人，都可以很容易地照着本文的描述，自己去操作一遍。
大概一周前，百度不是发布了一个“取得重要进展”的对话生成网络 PLATO-2 吗？我当时一看到那消息，精神就来了，为什么？这得先从解释一下“这玩意是干什么用的”说起——毕竟，这篇文章要让每一个群众都能看得懂，大家好才是真的好。
近日，百度发布对话生成网络 PLATO-2，宣布在开放域对话生成模型上迎来重要进展。PLATO-2 承袭 PLATO 隐变量进行回复多样化生成特性，模型参数高达 16 亿，涵盖中英文版本，可就开放域话题深度畅聊。实验结果显示，PLATO-2 中英文对话效果已超越谷歌 Meena、微软小冰和 Facebook Blender 等先进模型。
咳咳，这些专业术语说的是什么鬼？
如果你完全看不明白这段话，只需要知道：它说的是和NLP（自然语言处理，一门机器学习的分支学科）相关的一些东西。
可能有的人只听说过这段话里提到的“微软小冰”——她的主要功能就是一个【聊天机器人】，和小米的“小爱同学”颇为相似。
“小爱同学，帮我把空调打开！” “好的，开啦！”
——相信这样的场景，早已飞入我国千千万万寻常百姓家。
所以，百度发布的这个 PLATO-2，它可以用来做“小爱同学”的大脑，也就是最核心的那一块功能。不过现实中的“小爱同学”远比这个复杂，在这里只是做一个比喻而已。
[原创] PyTorch做inference/prediction的时候如何使用GPU
话不多说，直接进入主题。
✔ 判断能不能使用GPU
可能有多种原因会导致不能使用GPU，比如PyTorch安装的是CPU版的，显卡驱动没有正确安装等。下面的 if 语句在正常的情况下会返回 True：
if torch.cuda.is_available(): print('PyTorch can use GPU on current machine!')
文章来源：https://www.codelast.com/
✔ 设置模型使用GPU
model = MyModel(*args, **kwargs) model.load_state_dict(torch.load(your_model_file_path)) model.eval() # 设置成evaluation模式 if torch.cuda.is_available(): print('PyTorch can use GPU on current machine!') device = torch.device("cuda") model.to(device)
your_model_file_path 是模型文件的路径。
[原创] 总有一天，失业不再遥远
尽管人类离[通用人工智能]的路还很远，但越来越多新技术的出现，让这条路得以不断加速。
What？强化学习设计芯片？
就这几天的事：Google已经开始用强化学习技术来设计芯片了！
如果说用强化学习来玩游戏、下围棋，甚至用来帮助提升互联网广告的点击率、收入，都不是什么新鲜事的话，那么用强化学习来设计芯片，就也太新鲜了吧？但Google就做到了[1]：
我们提出了一种基于学习的芯片布局方法，这是芯片设计过程中最复杂、最耗时的阶段之一。与之前的方法不同，我们的方法具有从过去的经验中学习并随着时间的推移而改进的能力。特别是随着我们对更多的芯片块进行训练，我们的方法在快速生成以前未见过的芯片块的优化布局方面变得更好。为了实现这些结果，我们将芯片布局作为一个强化学习（RL）问题，并训练一个Agent将芯片网表的节点放置到芯片画布上。为了使我们的RL策略能够泛化到未见过的芯片块，我们将表征学习置于预测布局质量的有监督任务中。通过设计一个能够准确预测各种网表及其布局质量的神经架构，我们能够生成丰富的输入网表的特征嵌入。然后，我们使用这个架构作为我们的策略和价值网络的编码器来实现转移学习。我们的目标是将PPA（功率、性能和面积）降到最低，我们表明，在6个小时内，我们的方法可以在现代加速器网表上生成超越人类或可与之相媲美的芯片布局，而现有的基线需要人类专家在循环中进行，并需要几周的时间。
硬件工程师为之虎躯一颤。
[原创] 强化学习框架 rlpyt 的 size mismatch 错误原因及解决办法
查看关于 rlpyt 的更多文章请点击这里。
rlpyt 是BAIR(Berkeley Artificial Intelligence Research，伯克利人工智能研究所)开源的一个强化学习(RL)框架。我之前写了一篇它的简介。
当你使用 rlpyt 来实现自己的强化学习程序时，可能会遇到类似于下面这样的错误：
RuntimeError: size mismatch, m1: [1 x 365], m2: [461 x 32] at /tmp/pip-req-build-_357f2zr/aten/src/TH/generic/THTensorMath.cpp:752
本文分析错误原因及解决办法。
[原创] 强化学习框架 rlpyt 源码分析：(9) 基于CPU的并行采样器CpuSampler
查看关于 rlpyt 的更多文章请点击这里。
rlpyt 是BAIR(Berkeley Artificial Intelligence Research，伯克利人工智能研究所)开源的一个强化学习(RL)框架。我之前写了一篇它的简介。 本文是上一篇文章的续文，继续分析CpuSampler的源码。
我们已经知道了CpuSampler有两个父类：BaseSampler 和 ParallelSamplerBase。其中，BaseSampler主要是定义了一堆接口，没什么好说的，因此本文接着分析另一个父类 ParallelSamplerBase。在 ParallelSamplerBase 中，初始化函数 initialize() 做了很多重要的工作，已经够写一篇长长的文章来分析了，这正是本文的主要内容。
[原创] 强化学习框架 rlpyt 源码分析：(8) 基于CPU的并行采样器CpuSampler
写这篇文章的过程中，我改稿改到怀疑人生，因为有些我自己下的结论在看了很多次源码之后又自我否定了多次，所以这篇文章花了我很长时间才完工。虽然完稿之后我仍然不敢保证绝对正确，但这至少是在我当前认知情况下我“自以为”正确的版本了，写长稿不易，望理解。
查看关于 rlpyt 的更多文章请点击这里。
rlpyt 是BAIR(Berkeley Artificial Intelligence Research，伯克利人工智能研究所)开源的一个强化学习(RL)框架。我之前写了一篇它的简介。
在单机上支持丰富的并行(Parallelism)模式是 rlpyt 有别于很多其他强化学习框架的一个显著特征。rlpyt可以使用纯CPU，或CPU、GPU混合的方式来并行执行训练过程。