【正文】
函数的上界、下界：若 \(\exists M\) （不局限于正数）， \(s.t.\;f(x) \le M,\;\;\forall x \in I\) ，则称 \(f(x)\) 在区间 \(I\) 上有界。任何一个数 \(N > M\) ， \(N\) 也是 \(f(x)\) 的一个上界。
若 \(\exists P,\;\;s.t.\;\;f(x) \ge P,\;\;\forall x \in I\) ，则称 \(f(x)\) 在区间 \(I\) 上有下界。若 \(Q < P\) ，则 \(Q\) 也是一个下界。
\(f(x)\) 在区间 \(I\) 上有界 \( \Leftrightarrow f(x)\) 在 \(I\) 上既有下界又有上界（“ \( \Leftrightarrow \) ”表示充分必要条件）。
证明：
设 \(f(x)\) 在 \(I\) 上有界，根据定义， \(\exists M > 0,\;\;s.t.\;\;|f(x)| \le M,\;\;\forall x \in I\) 。
\(|f(x)| \le M \Leftrightarrow - M \le f(x) \le M\)
因此 \(f(x)\) 有下界 \(- M\) ，也有上界 \(M\) （对 \(\forall x \in I\) ）
反之，设 \(f(x)\) 在 \(I\) 上既有下界 \(m\) ，又有上界 \(N\) ，即 \(m \le f(x) \le N\)
如果 \(m = N = 0\) ，则 \(f(x) \equiv 0,\;\;\forall x \in I\)
因此 \(f(x)\) 在 \(I\) 上有界。
文章来源：http://www.codelast.com/
如果 \(m,N\) 不同时为零，取 \(M = \max \{ |m|,|N|\} > 0\) ，
则 \( - M \le - |m| \le m \le f(x) \le N \le |N| \le M\)
即 \( - M \le f(x) \le M \Rightarrow |f(x)| \le M,\;\forall x \in I\)
因此 \(f(x)\) 在 \(I\) 上有界。
2. 函数的单调性
若函数 \(f(x)\) 在区间 \(I\) 上，对任何 \({x_1},{x_2} \in I\) ，且 \({x_1} < {x_2}\) ，恒有 \(f({x_1}) < f({x_2})\) ，则称 \(f(x)\) 在 \(I\) 上是严格单调增的。
若 \({x_1} < {x_2}\) ，恒有 \(f({x_1}) \le f({x_2})\) ，则称 \(f(x)\) 在区间 \(I\) 上广义单调增（或直接称为单调增，或称非减的）。
若 \({x_1} < {x_2}\) ，恒有 \(f({x_1}) > f({x_2})\) ，则称 \(f(x)\) 在 \(I\) 上严格单调减。
类似地，也有广义单调减（单调减，非增的）的概念。
文章来源：http://www.codelast.com/
例如， \(y = {x^2},\;{D_f} = ( - \infty , + \infty )\)
在 \((0, + \infty )\) 上， \(y = {x^2}\) 严格单增。
在 \(( - \infty ,0)\) 上， \(y = {x^2}\) 严格单减。
又如，取整函数（取一个数的整数部分）：
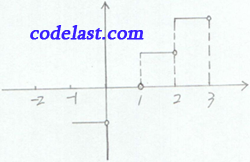
文章来源：http://www.codelast.com/
3. 函数的奇偶性
若 \(f(x)\) 在关于原点对称的区间 \(I\) 上满足 \(f( - x) = f(x)\) ，则称 \(f(x)\) 为偶函数。
若满足 \(f( - x) = - f(x)\) ，则称 \(f(x)\) 为奇函数。
偶函数图形关于 \(y\) 轴对称（例如： \(\cos x,\;{x^2}\) ）
奇函数图形关于原点对称（例如： \(\sin x,\;{x^3}\) ）
4. 函数的周期性
设 \(f(x)\) 的定义域为 \({D_f}\) ，如果存在非零的常数 \(T,\;s.t.\) 对任意的 \(x \in {D_f}\) ，有 \((x \pm T) \in {D_f}\) ，且 \(f(x + T) = f(x)\) ，则称 \(f(x)\) 为周期函数， \(T\) 称为 \(f(x)\) 的周期（通常周期是指最小正周期）。
文章来源：http://www.codelast.com/
四、 复合函数，反函数
1. 复合函数
设 \(y = \sqrt u ,\;\;u = 1 - {x^2}\) ，把 \(u = 1 - {x^2}\) 代入 \(y = \sqrt u \) 中，得到 \(y = \sqrt {1 - {x^2}} \) ，称为由 \(y = \sqrt u \) 与 \(u = 1 - {x^2}\) 复合而成的复合函数。
一般定义：
设 \(y = f(u)\) 是数集 \(Y\) 上的函数（ \(Y\) 是 \(f(u)\) 的定义域）， \(u = \varphi (x)\) 的定义域为 \(X\) ，值域为 \({Y_\varphi }\) ，且 \({Y_\varphi } \ne \Phi \) （ \(\Phi \) 表示空集）， \({Y_\varphi } \subseteq Y\) （表示 \({Y_\varphi }\) 是 \(Y\) 的子集），这时，对 \(\forall x \in X\) ，通过 \(u\) 都有唯一的 \(y\) 值与之对应，从而在 \(X\) 上产生一个新函数，用 \(f \cdot \varphi \) （中间是一个实心的点）表示，称 \(f \circ \varphi \) （中间是一个空心的圈）为 \(X\) 上的复合函数：
\(f\mathop \to \limits^{f \cdot \varphi } y\) ，或 \(y = f[\varphi (x)]\)
\(y = f[\varphi (x)]\) 的定义域：由 \(u = \varphi (x)\) 的定义域中使函数 \(u = \varphi (x)\) 的值域 \({Y_\varphi }\) 满足 \({Y_\varphi } \subseteq Y\) 的那一部分实数组成。
文章来源：http://www.codelast.com/
（第3课完）
文章来源：https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处：codelast.com
感谢关注我的微信公众号（微信扫一扫）：
