查看本系列文章合集,请点击这里。
在前面的文章中,我们看到,随机采样是一个蒙特卡罗方法中很关键的步骤。而采样是需要技巧的,单纯地增加采样次数太没有效率了,比如说,如果随机采样一亿次,你可以把结果计算得特别精确,但是采样一亿次需要的时间非常长,长得远远超过了我们能接受的范围,这又有什么意义呢?
人们发现,有一些方法可以让随机采的样本“特别好”。那么什么算“特别好”呢?比如说,本来使用没有任何原则的采样方法,需要采样1万个点,才能让计算出来的结果很接近真实值;现在使用一个“特别好”的采样方法,可以让我们只需要采样100个点,就可以让计算出来的结果很接近真实值了,这样就极大地减少了计算量。
而重要性采样(Importance Sampling),就是人们发现的、可以实现这个目的手段之一。
- 定义
重要性采样(Importance Sampling)是统计学中估计某一分布性质时使用的一种方法。该方法从与原分布不同的另一个分布中采样,而对原先分布的性质进行估计。
乍一看,这句话可能有点抽象,别急,往后看你就理解了。
- 实例——蒙特卡罗平均值法计算定积分
在之前的文章中,我们已经见识过了用蒙特卡罗投点法计算定积分的过程,这里有另一个叫作“平均值法”的方法,由于它也是随机化的算法,因此,它也属于一种蒙特卡罗方法。
文章来源:https://www.codelast.com/
我们来看看来自scratchapixel.com的一幅图:
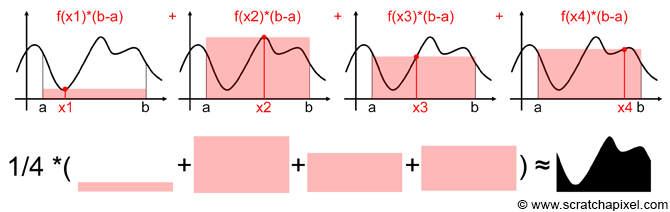
这幅图表明了什么意思呢?我们知道,计算[a,b]内的定积分就是求曲线 f(x)、直线 x=a,x=b以及x轴围成的形状的面积,因此,如果我们在曲线上随机地选取N个点,计算如图所示的粉红色长方形面积之和,再求个平均,其实就得到了定积分的近似值。点的数量取得越多,这个平均值就越逼近定积分的真实值。
用公式写出来就是:
![\frac{1}{N}\left[ {(b - a) \times f({X_1}) + (b - a) \times f({X_2}) + \cdots + (b - a) \times f({X_N})} \right] = \frac{{b - a}}{N}\sum\limits_{i = 1}^N {f({X_i})}](https://www.codelast.com/wp-content/plugins/latex/cache/tex_6729ad9b16ef416b8e9a493de61ad802.gif)
文章来源:https://www.codelast.com/
现在来看一下蒙特卡罗积分的表达式:

这个式子没有积分符号  ,但是它却叫做“积分”公式,这是因为这个式子求的是积分的近似值——当N越大的时候,计算出的值就越接近定积分的真实值。
,但是它却叫做“积分”公式,这是因为这个式子求的是积分的近似值——当N越大的时候,计算出的值就越接近定积分的真实值。
在公式中,有一个奇怪的东西,就是  ,它表示
,它表示  这个点,在某个分布下取
这个点,在某个分布下取  这个值的概率。那么这个分布是什么呢?比如说,它能不能是简单的均匀分布?后面我们会看到,这个分布是我们自己选取的。
这个值的概率。那么这个分布是什么呢?比如说,它能不能是简单的均匀分布?后面我们会看到,这个分布是我们自己选取的。
既然是要随机采样N个点,那么是不是随便用什么样的策略去采样,都可以达到同样的效果呢?这里用一幅图来说明,采样也是要讲究策略的,否则效果会很差:
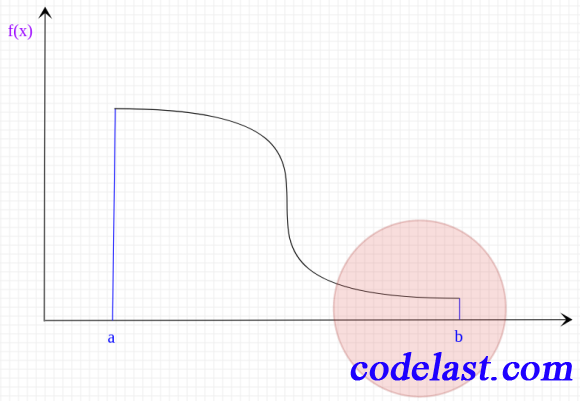
由于定积分值就是曲线下的面积,显然,如果我们采样的点恰巧大部分处于圆圈内,那么这些点下的面积之和必然比较小,此时,我们按前面所说的计算矩形面积的方法算得的积分值,是远远不能反映积分的真实值的。也就是说,圆圈处的点,对积分值的贡献小,靠近  处的曲线上的点,对积分值的贡献大。
处的曲线上的点,对积分值的贡献大。
所以,在实际采样的时候,靠近圆圈处的点应该少采一些,非圆圈处的点应该多采一些。
这就是重要性采样(Importance Sampling)的概念由来了——采样要按“重要性”来进行,不应该“平等对待”。
如果采样恰到好处的话,可能只需要进行很少的采样(计算若干个点的函数值),就可以求出误差很小的积分值。
- 参考文献
► 维基百科:重要性采样
► scratchapixel.com:Monte Carlo Methods in Practice
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
