牛顿法是最优化领域的经典算法,它在寻优的过程中,使用了目标函数的二阶导数信息,具体说来就是:用迭代点的梯度和二阶导数对目标函数进行二次逼近,把二次函数的极小点作为新的迭代点,不断重复此过程,直到找到最优点。
『1』历史
话说,牛顿法为什么叫牛顿法?这个近乎“废话”的问题,谁又真正查过?
Wiki里是这样写的:牛顿法(Newton's method)是一种近似求解方程的方法,它使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。
它最初由艾萨克•牛顿在《流数法》(Method of Fluxions,1671年完成,在牛顿死后的1736年公开发表)。
按我的理解,起初牛顿法和最优化没什么关系(在那个年代应该还没有最优化这门学科分支),但是在最优化研究兴起后,人们把牛顿法的思想应用在最优化领域,于是也就叫它牛顿法了。
『2』原理
下面我们就来推导一下牛顿法的实现。
目标函数  在点
在点  的泰勒展示式前三项为:
的泰勒展示式前三项为:

其中,  是一阶导数(梯度),
是一阶导数(梯度),  是二阶导数。当然,最后一项(高阶无穷小)我们依然是不考虑的。
是二阶导数。当然,最后一项(高阶无穷小)我们依然是不考虑的。
文章来源:http://www.codelast.com/
 为极小值点的一阶必要条件是:
为极小值点的一阶必要条件是:

由此便可得到迭代公式: 
在最优化line search的过程中,下一个点是由前一个点在一个方向d上移动得到的,因此,在牛顿法中,人们就顺其自然地称这个方向为“牛顿方向”,由上面的式子可知其等于: 
『3』优缺点
优点:充分接近极小点时,牛顿法具有二阶收敛速度——挺好的,不是么。
缺点:
①牛顿法不是整体收敛的。
②每次迭代计算  (的逆矩阵),计算量偏大。
(的逆矩阵),计算量偏大。
③线性方程组  可能是病态的,不好求解。
可能是病态的,不好求解。
(注:在代数方程中,有的多项式系数有微小扰动时其根变化很大,这种根对系数变化的敏感性称为不稳定性(instability),这种方程就是病态多项式方程)
为了解决“原始”牛顿法的这些问题,人们想出了各种办法,于是就有了下面的各种改进方案,请听我一一道来。
文章来源:http://www.codelast.com/
『4』牛顿法的改进1——阻尼牛顿法
前面说过了,牛顿法不是整体收敛的,在远离最优解时,牛顿方向  不一定是下降方向——而目标函数值“下降”就是最优化努力的方向,因此,人们想到了,可以在牛顿法迭代的过程中加入一点“阻力”:
不一定是下降方向——而目标函数值“下降”就是最优化努力的方向,因此,人们想到了,可以在牛顿法迭代的过程中加入一点“阻力”:

我觉得“阻力”这个词还是比较形象的——原来只有一个  ,现在多了一个
,现在多了一个  ,这就像是个阻碍啊。
,这就像是个阻碍啊。
问题是,  怎么求呢?
怎么求呢?
可以在确定  之后,利用line search技术,求出
之后,利用line search技术,求出  ,使之满足
,使之满足  (至于line search的算法,有太多太多了,这里有几个可以参考一下)。
(至于line search的算法,有太多太多了,这里有几个可以参考一下)。
满足了这个条件,会发生什么?
大家还记得《使用一维搜索(line search)的算法的收敛性》定理吗?仔细看里面的“适用于使用精确line search技术的算法”的收敛性定理,你就会发现,当满足了上面所说的条件时,(阻尼)牛顿法的整体收敛性就得到了保证。
当然,满足上面所说的条件的前提,就是所有的  都正定。因为如果
都正定。因为如果  不正定的话,就求不出
不正定的话,就求不出  ;求不出
;求不出  的话,就求不出
的话,就求不出  ;求不出
;求不出  的话,就求不出
的话,就求不出  ,因此就求不出迭代公式,寻优过程就无法进行。
,因此就求不出迭代公式,寻优过程就无法进行。
文章来源:http://www.codelast.com/
那么问题就来了:阻尼牛顿法确实offer了整体收敛性,但是它并没有解决一个问题:  不正定怎么办?此时迭代如何进行下去?因此,另一种改进方案应运而生,各位接着往下看。
不正定怎么办?此时迭代如何进行下去?因此,另一种改进方案应运而生,各位接着往下看。
『5』Goldstein-Price修正
首先,Goldstein和Price是两个人名,他们的具体生平事迹我没研究过。他们在1967年提出,如果  不正定(此时难以解出
不正定(此时难以解出  ),就用“最速下降方向”来作为搜索方向(看似已经“过时”的最速下降法还是能发挥余热的,这就体现出来了):
),就用“最速下降方向”来作为搜索方向(看似已经“过时”的最速下降法还是能发挥余热的,这就体现出来了):
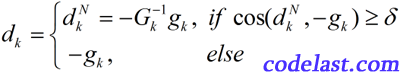
其中,

在这样的条件下,就使得
 总能满足
总能满足  ,从而也就满足了《使用一维搜索(line search)的算法的收敛性》定理中的“搜索方向条件”,从而(Goldstein-Price修正)牛顿法具有整体收敛性。
,从而也就满足了《使用一维搜索(line search)的算法的收敛性》定理中的“搜索方向条件”,从而(Goldstein-Price修正)牛顿法具有整体收敛性。文章来源:http://www.codelast.com/
『6』Goldfeld修正
与上面的Goldstein-Price修正的思路不同,Goldfeld在1966年也提出了一种方法,他的方法虽然还是在搜索方向
 上动手,但是当
上动手,但是当  不正定时,他不是用最速下降方向
不正定时,他不是用最速下降方向  来作为搜索方向,而是将
来作为搜索方向,而是将  修正成下降方向——用下面的式子:
修正成下降方向——用下面的式子:
其中,
 是一个正定矩阵,
是一个正定矩阵,  称为修正矩阵。在
称为修正矩阵。在  满足一定条件的时候,(Goldfeld修正)牛顿法具有整体收敛性。
满足一定条件的时候,(Goldfeld修正)牛顿法具有整体收敛性。具体要满足什么条件呢?一个关于矩阵
 “条件数”的条件。说实在的我对这部分不了解,并且这也不是本文的重点,所以在这里我就不把书上的定理搬上来了。
“条件数”的条件。说实在的我对这部分不了解,并且这也不是本文的重点,所以在这里我就不把书上的定理搬上来了。Goldfeld修正没有解决的问题就是:难以给出选取
 的有效方法。这就像是我告诉你,你要去魔法森林,就需要用到魔棒,但是魔棒去哪找,我不告诉你。于是,有其他的学者提出了其他的改进方法,帮你找到这个“魔棒”,请接着往下看。
的有效方法。这就像是我告诉你,你要去魔法森林,就需要用到魔棒,但是魔棒去哪找,我不告诉你。于是,有其他的学者提出了其他的改进方法,帮你找到这个“魔棒”,请接着往下看。文章来源:http://www.codelast.com/
『7』Gill-Murray的Cholesky分解法
看到这个小标题你可能就有点晕——请尽情地晕吧,这里光是人名就有三个。最重要的就是Cholesky,这里我要补充一个小插曲,给大家说点轻松的知识(从网上复制来的,链接不记得了):
Cholesky是一个法国数学家,生于19世纪末。Cholesky分解是他在学术界最重要的贡献。后来,Cholesky参加了法国军队,不久在一战初始阵亡。
Cholesky分解是一种分解矩阵的方法, 在线性代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积(那实数界来类比的话,此分解就好像求平方根)。与一般的矩阵分解求解方程的方法比较,Cholesky分解效率很高。
Gill和Murray这两个人,用Cholesky分解法实现了对牛顿法的改进,我个人觉得,他们的改进可以算是对Goldfeld修正的一种改进(或补充)吧,因为他们提供了求
 的方法。
的方法。
这里的Cholesky分解(牛顿法),是这么一回事:对  (即Hesse矩阵)进行Cholesky分解,在分解的过程中,对它进行一定的修正,最后得到近似的
(即Hesse矩阵)进行Cholesky分解,在分解的过程中,对它进行一定的修正,最后得到近似的  ,把这个
,把这个  当作
当作  ,用于解出
,用于解出  。
。
文章来源:http://www.codelast.com/
至于这个修正过程的具体做法,我只能说我不甚清楚,我不想在这里误导大家,只想把我自己理解的写下来:
若  为正定矩阵,则它总能进行Cholesky分解,即
为正定矩阵,则它总能进行Cholesky分解,即  ,其中
,其中  是一个单位下三角矩阵,
是一个单位下三角矩阵,  是一个对角矩阵(diagonal matrix,除主对角线外的元素均为0的方阵)。
是一个对角矩阵(diagonal matrix,除主对角线外的元素均为0的方阵)。
若  不是个正定矩阵,那么就让Chokesky分解过程满足
不是个正定矩阵,那么就让Chokesky分解过程满足  (
(  是一个对角矩阵),并且在分解过中调整
是一个对角矩阵),并且在分解过中调整  对角线上的元素(人们总结出了一些调整方法,例如使这些元素>某个正常数),使得Hesse矩阵正定——这里说的Hesse矩阵,是指前面说的
对角线上的元素(人们总结出了一些调整方法,例如使这些元素>某个正常数),使得Hesse矩阵正定——这里说的Hesse矩阵,是指前面说的  。分解完成后,就可以用
。分解完成后,就可以用  来解出
来解出  了。
了。
如果  是个充分正定(书上的名词,谁能给解释一下?)的矩阵,那么经过这个修正的过程,
是个充分正定(书上的名词,谁能给解释一下?)的矩阵,那么经过这个修正的过程,  其实就是原来的
其实就是原来的  ,
,  其实也就不存在了——这是个很好的特性。
其实也就不存在了——这是个很好的特性。
我感觉上面的修正过程,用妹子来做一个比喻就是:一个妹子本来已经长得挺漂亮了,你为她化个妆(只要不是故意黑她),她还是那么漂亮。反之,如果一个妹子长得很搓,那么,你为她化妆,是有可能让她看上去变靓的。总之,都得到了我们想要的结果。
Cholesky分解算法我没看过,这里就没办法说了。
有书上说,Gill-Murray的Cholesky分解牛顿法是“对牛顿法改造得最彻底、最有实用价值的方法”。
看来,有时候真的是:最复杂的就是最好的,没有捷径可走啊。
文章来源:http://www.codelast.com/
『8』信赖域牛顿法
在这篇解释信赖域算法的文章里,我们说过了,信赖域算法具有整体收敛性。利用这一点,可以将其与牛顿法“合体”,创造出具有整体收敛性的信赖域牛顿法,即,我们要求的问题是:
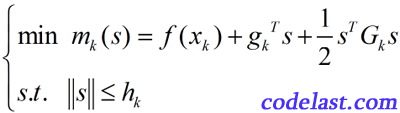
其中,
 为位移,
为位移,  表示第k次迭代,
表示第k次迭代,  为梯度,
为梯度,  为Hesse矩阵(二阶导数矩阵),
为Hesse矩阵(二阶导数矩阵),  为第k次迭代时的信赖域上界(半径)。
为第k次迭代时的信赖域上界(半径)。为什么它叫信赖域牛顿法?首先,它没有line search,求的是位移s,所以是一种信赖域算法;其次,它在求解的时候用到了梯度和二阶导数,因此是一种牛顿法。所以整体上叫它信赖域牛顿法是讲得过去的。
信赖域牛顿法有一个特点是令人欣慰的:没有要求
 (即Hesse矩阵)必须正定,这与前面各种算法与
(即Hesse矩阵)必须正定,这与前面各种算法与  正定那些纠缠不清的关系有很大不同。
正定那些纠缠不清的关系有很大不同。至于信赖域算法的具体求解步骤是怎样的,这里就不说了,还是请大家参考这篇文章。
文章来源:http://www.codelast.com/
『9』总结
对牛顿法及其众多改进的介绍就到这里结束了。大家会看到,里面有很多定理没给出证明,有些推导可能也不够严谨,但是它们的结论基本上是正确的,如果纠结于细节,那真的是要去做理论研究,而不是应用到工程实践了。所以,学习最优化的时候,我们可以在一定程度上“着眼全局,忽略细节”,这会极大地有助于理解。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

Newton 和 Taylor 的时代差别不大。Taylor 的结果,Newton 是知道的,诸如 arcsin x 函数(之后是 sin x 函数)的级数展开式都是 Newton 获得的,没有什么问题。
利用泰勒公式推牛顿法有些不科学。牛顿比泰勒早出生,还是用牛顿原始的方法比较好
Newton 和 Taylor 的时代差别不大。Taylor 的结果,Newton 是知道的,诸如 arcsin x 函数(之后是 sin x 函数)的级数展开式都是 Newton 获得的,没有什么问题。
你这个理由太有趣了,按你这个理论,所有早期人类发现的现象都不应该用现在新发现的规律去解释啦哈哈.