查看本系列文章合集,请点击这里。
为了对蒙特卡罗方法有一个直观的印象,我们先举一个实例(计算圆周率  ),让从来没有接触过蒙特卡罗方法的人产生“原来这就是Monte Carlo”的感觉,以减少刚开始学习的困惑。
),让从来没有接触过蒙特卡罗方法的人产生“原来这就是Monte Carlo”的感觉,以减少刚开始学习的困惑。
- 非蒙特卡罗方法
圆周率  可以怎么计算?其中一个“常规”的方法就是利用
可以怎么计算?其中一个“常规”的方法就是利用  的莱布尼茨公式:
的莱布尼茨公式:

不断增大  的值,就能越来越逼近
的值,就能越来越逼近 
当  的最大值取30000时,可以计算得
的最大值取30000时,可以计算得 
- 蒙特卡罗方法
相比之下,用蒙特卡罗方法来计算  ,可能就是一个比较“另类”的途径了。
,可能就是一个比较“另类”的途径了。
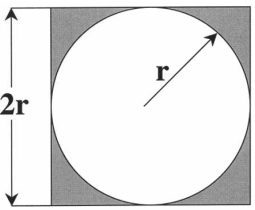
假设圆外部有一个相切的正方形,如下图所示:
文章来源:https://www.codelast.com/
设圆面积为C,正方形面积为S,则利用面积公式可以轻易算得: 
然后,我们在正方形内随机生成30000个点(当然可以生成更多,这里只是用30000举个例子),分别计算这些点与圆心的距离,距离<r 表示点在圆内部:

文章来源:https://www.codelast.com/
从面积之比可知:如果点是均匀分布的,则圆内的点的数量应该占所有点数量的  ,计算数量之比,再乘以4,即可得圆周率。
,计算数量之比,再乘以4,即可得圆周率。
在某一次实验中,模拟30000个点,  的估算值与真实值相差0.07%
的估算值与真实值相差0.07%
所以,这里正是巧妙地利用了“随机”这个技术,来计算了圆周率,这种方法就属于蒙特卡罗方法。
- 参考文献
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
