【正文】
<定义2> 设函数  在
在  点的左侧
点的左侧 ![[{x_0} + \Delta x,{x_0}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_f11dc0ddbf2a74d4f03cb82a49cff880.gif) (
(  )有定义,如果极限
)有定义,如果极限  存在,则称此极限为
存在,则称此极限为  在
在  点的左导数,记为
点的左导数,记为 
类似有右导数:

显然有:
 在
在  点可导
点可导  存在且
存在且 
文章来源:http://www.codelast.com/
如果  在
在  内可导,且
内可导,且  和
和  存在,则称
存在,则称  在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上可导,记为
上可导,记为 ![f(x) \in D\left[ {a,b} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_b378f88b771c9de188c8f37fd89b292b.gif)
三、导数的几何意义
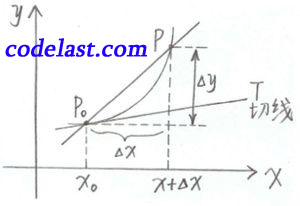
由实例2(曲线上一点处切线的斜率问题)及导数定义:

可知  表示割线
表示割线  的斜率
的斜率

文章来源:http://www.codelast.com/
 在几何上表示曲线上一点
在几何上表示曲线上一点  点处切线
点处切线  的斜率
的斜率  ,
,  是切线
是切线  的倾角。
的倾角。
根据导数几何意义及平面解析几何关于直线方程的知识(点斜式方程):
切线方程为: 
曲线上点  的法线(过
的法线(过  点且与该点处的切线垂直的直线,称为曲线在
点且与该点处的切线垂直的直线,称为曲线在  点的法线)方程是什么?
点的法线)方程是什么?
已知:切线斜率 
而切线与法线垂直,故法线斜率  (与切线斜率互为负倒数,其中
(与切线斜率互为负倒数,其中  )
)
所以法线方程为: 
若  在
在  点处
点处  (表示切线垂直于
(表示切线垂直于  轴),则切线方程为
轴),则切线方程为 
文章来源:http://www.codelast.com/
例1. 求曲线  在
在  处的切线方程和法线方程。
处的切线方程和法线方程。
解:先求导数:  ,则
,则 
切线斜率  ,法线斜率
,法线斜率 
因此切线方程为: 
法线方程为: 
文章来源:http://www.codelast.com/
思考:曲线  外有一点
外有一点  ,过
,过  点作曲线的切线,怎样求该切线的方程?
点作曲线的切线,怎样求该切线的方程?
四、函数的可导性与连续性的关系
<定理> 如果函数  在
在  点可导,则
点可导,则  在
在  点必定连续。
点必定连续。
证:设  的自变量
的自变量  在
在  点有增量
点有增量  ,函数对应的增量
,函数对应的增量 
要证  在
在  点处连续,也就是要证
点处连续,也就是要证  (注:为什么?见第18课的连续性定义)
(注:为什么?见第18课的连续性定义)
由于  在
在  点可导,从而有:
点可导,从而有:  存在,且
存在,且 
根据有极限的函数与无穷小的关系(  )可知:
)可知:

即: 
两边取极限:

(注:  为两个无穷小的乘积,仍为无穷小)
为两个无穷小的乘积,仍为无穷小)
因此函数  在
在  点处连续(连续是可导的必要条件)
点处连续(连续是可导的必要条件)
定理的逆命题不成立,即函数在一点连续,也不一定是可导的。
文章来源:http://www.codelast.com/
(第23课完)
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
