实现Powell算法的基础之一:你需要至少先掌握一种一维极值搜索算法。比较流行的是Golden Ratio Search(黄金比例搜索法),Fibonacci Search(斐波纳契搜索法),等等。
问:Powell算法有什么用?
答:Powell是一种非常稳健的非线性最优化算法(当然,整个求解过程中需要一些辅助的技巧,否则可能达不到“稳健”标准)。非线性最优化有什么用?这个问题实在太大了,举个简单的例子来说,你的业务每天会产生类似的一批数据,你知道它们冥冥中可能符合一些“规律”,这些规律可以用一个数学模型来描述,通俗地说就是可以用一个函数来表示自变量和因变量的关系,但是你又不确定这个关系的比较准确的形式是什么,那么这个时候,你就需要想办法来找出这个关系,此时你就需要先估计一个数学模型,再用你已经得到的数据来做验证。但是你估计的数学模型中,含有一些未知的参数,例如,你猜测的数学模型为y=aX2+bX+c,但是对每一批数据来说,a、b、c可能是不同的,如何求出这几个参数的值呢?“最优化”算法就可以解决这种问题。
首先,你要知道使用相当广泛的最小二乘法,它的简单理论依据可以看我的这篇文章。
为什么要谈及最小二乘呢?道理很简单,如下:假设你今天产生的一批数据点(x,y)为:
X Y
1 16
0.8 14
1.3 23
1.9 19
同时假设理想的数学模型(式中的3、7、6当前是未知的,需要求出来)为:y=3x2+7x+6
显而易见,只有第1个数据点完全符合这个数学模型,其他3个点都不能完全符合,即:方程组
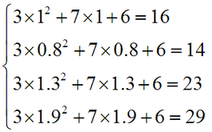
是一个超定方程组(overdetermined systems),求不出精确解。我们只能求出一个近似解,使得这个近似解是“最优”的。那么这个“最优”的判断标准是什么?上文链接中的最小二乘就是一种,详情可以查看我链接中的文章。
知道了提及最小二乘的原因,下面我们如何求出数学模型y=ax2+bx+c中的a、b、c呢?Powell算法来也。
注意,我们此处的数学模型可谓是简单至极,只有一个自变量x,但在实际的复杂系统中,我们经常会遇到自变量是N维(N>1)的情况,Powell算法可以轻松地解决多维情况下的最优化,当然,对一维的特殊情况也不在话下了。为了描述清晰,我们还是以N维自变量的情况作为我们讨论的基础,否则将无以体现算法的通用性。
整个Powell求解过程涉及到诸多技术,包括极值划界(别以为简单,信不信能折腾死你)、一维线性搜索、共轭方向集的选取及更新、各种迭代终止的条件判断、保证收敛以及加速收敛的一系列处理等等,实在不是一句两句就可以说得清楚,甚至于,在你不是一个对相关数学知识很熟练的人的情况下,对很多解释,你都可能要看很多遍才能看明白,因此我这篇文章也不可能几天就完成。有时间的话我会一点点补充。据某些文章称,在非线性优化方面,经过改进的LM算法可比Powell算法更强。不过,研究这些理论远不像吃饭喝水那么简单,能掌握一种稳健且足够高效的算法足以完成我们几乎所有工作了。
网上有很多人求代码,求人给他解释某些下载到的代码中各参数的含义,就我个人的经验,我可以很肯定地说,目前,你能在网上找到的所有公开的、带中文注释的Powell算法的源码,都不足以让你理解Powell算法(除非你本来就懂),甚至于那些代码你拿到了都不知道怎么用。因此,你必须静下心来一点一点地看算法的原理,拆分为一个个逻辑块来研究。
Powell方法是一种“共轭方向”法,既然说到了共轭方向,就必须要解释其含义。
来自网上的一段定义如下(http://www.tyywlk.cn/kscx/youhuasheji/index.asp):
设A为 n×n 阶实对称正定矩阵,如果有两个 n 维向量S1和S2满足:
S1TAS2 = 0
则称向量S1与S2对于矩阵A共轭。如果A为单位矩阵,则上式即成为,这样两个向量的点积(或称内积)为零,此二向量在几何上是正交的,它是共轭的一种特例。
设A为对称正定矩阵,若一组非零向量S1,S2,……,Sn满足
SiTASj = 0
则称向量系为关于矩阵A共轭。共扼向量的方向称为共轭方向。
上面就是“共轭方向”的定义。
说得形象一点,共轭方向就是不会“互相影响”的方向。我来举一个例子,假设你在平地上走路,想从A地点走到B地点,但是我规定你走的每一步与下一步都不能互相影响,请问你该如何走?那么,你可以先水平地走一段路,再垂直地走一段路,再水平地走一段路……这样,每一步与下一步都不会互相影响了。反之,如果你先沿非水平的方向走了一段路,又沿垂直的方向走了一段路,则:在非水平方向上走的那段路,其实是对垂直方向走的那段路是有影响的,因为它不是水平的,所以它有垂直方向上的分量,因此相当于你在垂直方向上也走了一段分量的路。这就是”相互影响“的例子。我说的这种例子太生活化,可能不严谨,但是应该比那些公式更有助于你理解问题。
为什么基于共轭方向的搜索算法可以到达极值点?这要从二次正定函数开始说了。再转一段网上的话:
共轭方向在最优化问题中的应用是基于其具有一个重要性质,即:设S1,S2,…,Sn是关于A的n个互相共轭的向量,则对于求正定二次函数f(X)=c+bTX+(XTAX)/2的极小点,只需从任意初始点出发,依次沿Si(i=1,2,…,n)方向进行一维最优化搜索,至多n步便可以收敛到极小点,其最后所达的点必是n维正定二次目标函数的极小值点。
正定二次函数的一般形式为
f(X)=c+bTX+(XTAX)/2
式中:A为n×n阶对称正定矩阵; c为实常数;b=[b1,b2,…,bn]T为常列向量;X=[X1,X2,…,Xn]T为变列向量。
当维数n=2时,为二维正定二次函数。
简言之,用共轭方向法对于二次函数从理论上来讲,n步就可达到极小点。因而说共轭方向法具有有限步收敛的特性。通常称具有这种性质的算法为二次收敛算法。
理论与实践证明,将二次收敛算法用于非二次的目标函数,亦有很好的效果,但迭代次数不一定保证有限次,即对非二次n维目标函数经n步共轭方向一维搜索不一定就能达到极小点。在这种情况下,为了找到极小点,可用泰勒级数将该函数在极小点附近展开,略去高于二次的项之后即可得该函数的二次近似。实际上很多的函数都可以用二次函数很好地近似,甚至在离极小点不是很近的点也是这样。故用二次函数近似代替非二次函数来处理的方法不仅在理论分析上是重要的,而且在工程实际应用中也是可取的。
这就是我们在共轭方向上进行搜索的原因。
需要注意的是,由于在搜索的过程中,某些共轭方向可能会变得线性相关,导致“共轭”性质丢失,使得搜索失效,因此,我们需要用一定的策略来调整共轭方向集中的方向,使得搜索可以收敛到正确的点。
最显而易见的共轭方向集就是单位矩阵中的每个列向量构成的方向集,因为这些向量两两之间肯定是共轭的,因此,初始的搜索方向就从他们开始,并不断进行方向的调整。
在方向集的一个方向上搜索时,就相当于在一维方向上搜索极值,这就是前面所说的一维极值搜索算法干的事情了。由于要求得极值,我们必然要对函数值进行计算,在一维情况下,就是求y=f(x,p)——求函数值非常简单。但由于我们的自变量是多维的(亦即:是一个向量),因此,在每一次求函数值的过程中,我们要把多维方向的“点”映射到一维方向上的点上,所以我们需要这样一个C++函数,使得我们输入一个向量X,可以返回对应的函数值f(X),来完成这个工作。有了这个基础,我们才能实现在一个方向上的极值搜索。
其实,在不考虑通用性的情况下,这个映射函数也可以不要,你只要在C++程序中每一个需要计算函数值的地方,都把你要最优化的函数形式直接代入就行了。不过,我们想要实现的最终效果是:用户只需要在软件界面上编写一个数学函数式,再输入数据,就可以进行计算了,这样的话映射函数就起作用了。
文章来源:http://www.codelast.com/
补充:
写过上面的文字很久之后,再来重新看这篇文章,发现自己以前真的是写了很多“废话”,但愿没有让读者更晕。下面就补充一下Powell共轭方向集方法到底是怎么获取到一个共轭方向集的:
-
假设我们最终找到的共轭方向集为
 ,但开始总要有一个初始的方向集,我们选择基向量(单位向量)
,但开始总要有一个初始的方向集,我们选择基向量(单位向量)  作为初始方向集
作为初始方向集 -
设初始点为

-
将
 这些点分别移动到
这些点分别移动到  方向上的极小点处(通过line search),这些点分别记为
方向上的极小点处(通过line search),这些点分别记为 
-
置方向

-
置方向

-
将
 移动到方向
移动到方向  上的极小点处,记为
上的极小点处,记为  ,依次迭代下去
,依次迭代下去
Brent(就是Brent's method的那个作者)证明了以上方法是可行的。
看上面的文字描述,可能大多数人仍然不清楚具体的过程是怎么做的,我建议找一份Powell方法的代码来看一下,细想一下,恐怕才能理解。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

博主写的很通俗,关注了。有个小建议,加上个例子就更好理解了!
楼主的解释太精妙了。适合处女座的人阅读!
鲍威尔(Powell)算法确实是非常稳健和高效的,相比与同级别的LM算法,还省去了求方程组的Jacobi矩阵。
最近做了一个48个方程组、5个待求量的最小二乘问题,在同样的初始点下,Powell算法耗时20ms,LM算法耗时300ms+。而且LM算法的Jacobi矩阵是事前求好写入的,但也没能加快速度。
环境:VS2010 库:Eigen
非线性最小二乘问题比较经典的有gauss-newton法,LM法,不过看了你写的POWELL算法,感觉也不错
我有个问题想请教你:
我的模型是很复杂的隐函数,但我只回归一个参数,我能不能用powell法或者单纯形法搜索法做?
powell法或者单纯形法搜索法是针对多个未知数的,如果只有一个的话, 就是一维的,那么用这两个方法与专门的一维搜索法(比如0.618法之类的)比,哪个的效果要好?
如果只求一个未知数,单纯形法可以做。powell好像不行。我感觉的,不知对不对?
赞~写的不错,今天刚看了Powell method,Golden ratio search 和 Fibonacci search~
请问什么时候更新未完的部分呢?很受益
谢谢支持。不过我最近很忙,有时间才能继续补充。
解释的很好