《Neural Networks and Deep Learning》一书的中文译名是《神经网络与深度学习》,书如其名,不需要解释也知道它是讲什么的,这是本入门级的好书。
在第一章中,作者展示了如何编写一个简单的、用于识别MNIST数据的Python神经网络程序。对于武林高手来说,看懂程序不会有任何困难,但对于我这样的Python渣则有很多困惑。所以我对做了一些笔记,希望同时也可以帮助有需要的人。
『1』原文及程序
在这里,先把中译版部分贴上来,以方便后面的笔记记录(这只是一部分):
在给出一个完整的清单之前,让我解释一下神经网络代码的核心特征,如下。核心是一个Network类,我们用来表示一个神经网络。这是我们用来初始化一个Network对象的代码:
class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]
net = Network([2, 3, 1])
 。矩阵中的
。矩阵中的  是连接第二层的
是连接第二层的  神经元和第三层的
神经元和第三层的  神经元的权重。
神经元的权重。
『2』程序解读
正如上面的代码示例,创建一个Network对象的时候,传入的是一个list,例如 [2, 3, 1],list中有几个元素就表示神经网络有几层,从list中的第一个元素开始,每一个元素依次表示第1层、每2层、……第n层的神经元的数量。
这个不难理解,比较难理解的是 bias(偏差)以及 weight(权重)的表示方式。
文章来源:https://www.codelast.com/
我们先来看 bias(偏差):
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
首先需要明确的是,中括号表明了 biases 是一个list,中括号里的内容是对这个list进行赋值的代码,它采用了一个for循环的方式来赋值,例如下面的代码:
a = [i for i in range(3)] print(a)
会输出结果:
[0, 1, 2]
所以,np.random.randn(y, 1) for y in sizes[1:] 这部分代码表达的就是—— list中的每一个元素都是 np.random.randn(y, 1) 这个表达式的计算结果,而这个表达式是含有变量 y 的,y 必须要有实际的值才能计算,所以用一个for循环来给 y 赋值,y 能取的所有值就是对 sizes[1:] 这个list进行遍历得到的。前面已经说过了,sizes本身是一个list,而sizes[1:] 表示的是取这个 list 从第2个元素开始的子集,给个例子:
a = [5, 6, 8] print(a[1:])
会输出:
[6, 8]
所以,在我们前面用 net = Network([2, 3, 1]) 这样的代码来创建了一个对象之后,sizes[1:] 的内容其实就是 [3, 1],所以 y 的取值就是 3 和 1,所以 biases 这个list的第一个元素就是 np.random.randn(3, 1),第二个元素就是 np.random.randn(1, 1)。
文章来源:https://www.codelast.com/
我觉得经过这样解释,biases 在结构上看来是什么东西已经比较清楚了吧?
那么话说回来,我们虽然知道了 np.random.randn(3, 1) 是 biases 的第一个元素,但 np.random.randn() 又是什么鬼?
且听我道来:
np 是这个Python程序 import 进来的Numpy库的缩写:
import numpy as np
randn() 是Numpy这个库中,用于生成标准正态分布数据的一个函数。其实 randn(3, 1) 生成的是一个3x1的随机矩阵,我们可以在Python命令行中直接试验一下:
import numpy as np np.random.randn(3, 1)
输出结果如下:
array([[ 1.33160979],[ 0.66314905],[ 0.27303603]])
可见,它输出的是一个3行,1列的随机数矩阵——你看这输出多体贴,为了表明“3行1列”,它没有把数字都排在一行,而是特意放在了3行里。
好了,现在我们已经彻底了解了 biases 的结构,那么再来看看,为什么它的第一个元素是3x1的矩阵,第二个元素是1x1的矩阵呢?
这跟要创建的神经网络层的结构有关。
文章来源:https://www.codelast.com/
如作者书中所说,“假设第一层神经元是一个输入层,并对这些神经元不设置任何偏差,因为偏差仅在之后的层中使用”,所以 biases 只有两个元素,而不是3个。但知道了这一点并不能解决我们心中的疑惑:为什么 biases[0] 是一个 3x1 的矩阵,biases[1] 是一个 1x1 的矩阵呢?
这就跟weight(权重)有关了,所以,我们不妨先来看看代码中,weight是如何定义的:
self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]
这个冗长的实现需要“细细品味”。
首先,中括号表明 weights 是一个list,中括号里的代码对这个list的每一个元素进行赋值,list中的每一个元素都是一个 np.random.randn(y, x) ——这个东西我们刚才在解释 biases 的时候已经说过了,它是一个y行x列的随机数矩阵。那么y和x的具体值又是什么呢?它们是由for循环定义的:
for x, y in zip(sizes[:-1], sizes[1:])
首先要注意,这里是按 x, y 的顺序来赋值的,而不是 y, x,这和 np.random.randn(y, x) 中的顺序相反。
其中,zip()是Python的一个内建函数,它接受一系列可迭代的对象(例如,在这里是两个list)作为参数,将对象中对应的元素打包成一个个tuple(元组),然后返回由这些tuples组成的list。
为了形象地说明zip()的作用,我们来看看这句简单的代码:
zip([3, 4], [5, 9])
它的输出是:
[(3, 5), (4, 9)]
可见,zip() 分别取出 [3, 4] 以及 [5, 9] 这两个 list 的第一个、第二个元素,然后合成了两个 tuple:(3, 5) 和 (4, 9),然后再把这两个tuple组成一个list:[(3, 5), (4, 9)]。所以,假设我们有如下代码:
for x, y in zip([3, 4], [5, 9])
那么 x, y 的取值就有两组了:3, 5 和 4, 9。
有了这样直观的对比,我们已经可以理解 for x, y in zip(sizes[:-1], sizes[1:]) 是什么含义了。其实 sizes 就是一个含有3个元素的list:[2, 3, 1],因此 sizes[:-1] 就是去掉最后一个元素的子list,即 [2, 3];而 sizes[1:] 就是去掉第一个元素的子list,即 [3, 1]。
所以现在真相大白:x, y 的取值有两组,一组是 2, 3,另一组是 3, 1。
再回去看 weights 的赋值代码,于是可以秒懂:weights 的第一个元素 weights[0] 是一个 3x2 的随机数矩阵,weights 的第二个元素 weights[1] 是一个 1x3 的随机数矩阵。
文章来源:https://www.codelast.com/
现在总结一下:
biases[0]:3x1 的矩阵
biases[1]:1x1 的矩阵
weights[0]:3x2 的矩阵
weights[1]:1x3 的矩阵
虽然我们已经精确分析出了那段代码的含义,但有人可能还是要问:为什么创建的bias和weight是这些维度的?
为了能帮助理解,我们画出这个神经网络的结构(第一层有2个神经元,第二层有3个神经元,最后一层有1个神经元):
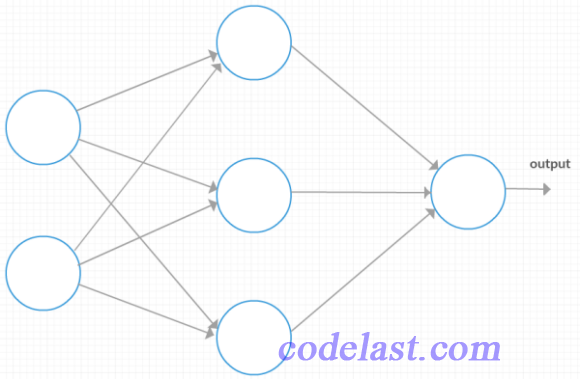
文章来源:https://www.codelast.com/
从图上我们可以一眼看出,第一层的输入向量(也就是  中的
中的  )是一个2行1列的向量,或者说是一个 2x1 的矩阵;第二层的
)是一个2行1列的向量,或者说是一个 2x1 的矩阵;第二层的  是一个3行1列的向量,或者说是一个 3x1 的矩阵。
是一个3行1列的向量,或者说是一个 3x1 的矩阵。
我们知道,除了输出层(output)之外,每一层的输入  都要经过一个
都要经过一个  的运算(这里忽略了激励函数),得到一个矩阵,作为下一层的输入。式中既然有weight(w)和
的运算(这里忽略了激励函数),得到一个矩阵,作为下一层的输入。式中既然有weight(w)和  向量的点乘,weight矩阵的列数就必须和
向量的点乘,weight矩阵的列数就必须和  向量的行数相等,所以这里是不是恰好符合这个规则呢?
向量的行数相等,所以这里是不是恰好符合这个规则呢?
来看看:
第一层→第二层的  运算就是 weight[0]矩阵
运算就是 weight[0]矩阵  + biases[0] 矩阵,即 (3x2矩阵)
+ biases[0] 矩阵,即 (3x2矩阵)  (2x1矩阵) + (3x1矩阵),结果是一个 3x1 的矩阵,这个矩阵,作为下一层的输入,实际上就是下一层的
(2x1矩阵) + (3x1矩阵),结果是一个 3x1 的矩阵,这个矩阵,作为下一层的输入,实际上就是下一层的  。前面我们分析过,第二层的
。前面我们分析过,第二层的  应该是一个 3x1 的矩阵,这与运算结果完全相符。
应该是一个 3x1 的矩阵,这与运算结果完全相符。
第二层→第三层的  运算就是 weight[1]矩阵
运算就是 weight[1]矩阵  + biases[1] 矩阵,即 (1x3矩阵)
+ biases[1] 矩阵,即 (1x3矩阵)  (3x1矩阵) + (1x1矩阵),结果是一个 1x1 的矩阵,其实就是一个标量,由于后面已经没有其他层,所以这个标量就是整个神经网络的output。
(3x1矩阵) + (1x1矩阵),结果是一个 1x1 的矩阵,其实就是一个标量,由于后面已经没有其他层,所以这个标量就是整个神经网络的output。
通过以上不厌其烦的分析,相信任何人都能搞明白那仅有不到10行的代码是如何巧妙地定义了一个神经网络,搞定!
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

怎么注册啊
感谢如此细致的讲解
求全系列的《Neural Networks and Deep Learning》读书笔记的更新,讲的实在太好了。
太棒了,什么时候更新