line search(一维搜索,或线搜索)是最优化(Optimization)算法中的一个基础步骤/算法。它可以分为精确的一维搜索以及不精确的一维搜索两大类。
在本文中,我想用“人话”解释一下不精确的一维搜索的两大准则:Armijo-Goldstein准则 & Wolfe-Powell准则。
之所以这样说,是因为我读到的所有最优化的书或资料,从来没有一个可以用初学者都能理解的方式来解释这两个准则,它们要么是长篇大论、把一堆数学公式丢给你去琢磨;要么是简短省略、直接略过了解释的步骤就一句话跨越千山万水得出了结论。
每当看到这些书的时候,我脑子里就一个反应:你们就不能写人话吗?
我下面就尝试用通俗的语言来描述一下这两个准则。
Armijo-Goldstein准则的核心思想有两个:①目标函数值应该有足够的下降;②一维搜索的步长α不应该太小。
文章来源:http://www.codelast.com/
有了这两个指导思想,我们来看看Armijo-Goldstein准则的数学表达式:
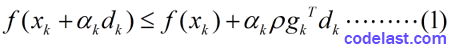
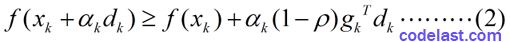
其中, 
文章来源:http://www.codelast.com/
(1)为什么要规定  这个条件?其实可以证明:如果没有这个条件的话,将影响算法的超线性收敛性(定义看这个链接,第4条)。在这个速度至关重要的时代,没有超线性收敛怎么活啊!(开个玩笑)
这个条件?其实可以证明:如果没有这个条件的话,将影响算法的超线性收敛性(定义看这个链接,第4条)。在这个速度至关重要的时代,没有超线性收敛怎么活啊!(开个玩笑)
具体的证明过程,大家可以参考袁亚湘写的《最优化理论与方法》一书,我没有仔细看,我觉得对初学者,不用去管它。
(2)第1个不等式的左边式子的泰勒展开式为:

去掉高阶无穷小,剩下的部分为: 
而第一个不等式右边与之只差一个系数 
我们已知了  (这是
(这是  为下降方向的充要条件),并且
为下降方向的充要条件),并且  ,因此,1式右边仍然是一个比
,因此,1式右边仍然是一个比  小的数,即:
小的数,即:

也就是说函数值是下降的(下降是最优化的目标)。
文章来源:http://www.codelast.com/
(3)由于  且
且  (
(  是一个下降方向的充要条件),故第2个式子右边比第1个式子右边要小,即:
是一个下降方向的充要条件),故第2个式子右边比第1个式子右边要小,即:

如果步长  太小的话,会导致这个不等式接近于不成立的边缘。因此,式2就保证了
太小的话,会导致这个不等式接近于不成立的边缘。因此,式2就保证了  不能太小。
不能太小。
(4)我还要把很多书中都用来描述Armijo-Goldstein准则的一幅图搬出来说明一下(亲自手绘):
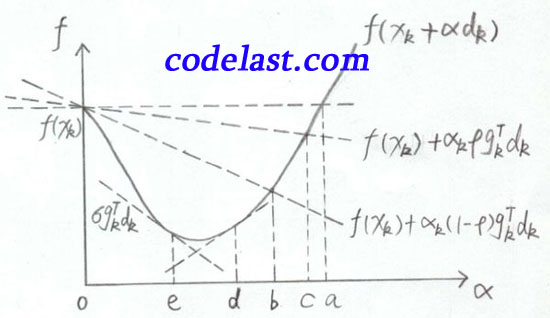
文章来源:http://www.codelast.com/
横坐标是  ,纵坐标是
,纵坐标是  ,表示在
,表示在  均为常量、
均为常量、  为自变量变化的情况下,目标函数值随之变化的情况。
为自变量变化的情况下,目标函数值随之变化的情况。
之所以说  均为常量,是因为在一维搜索中,在某一个确定的点
均为常量,是因为在一维搜索中,在某一个确定的点  上,搜索方向
上,搜索方向  确定后,我们只需要找到一个合适的步长
确定后,我们只需要找到一个合适的步长  就可以了。
就可以了。
当  为常量,
为常量,  为自变量时,
为自变量时,  可能是非线性函数(例如目标函数为
可能是非线性函数(例如目标函数为  时)。因此图中是一条曲线。
时)。因此图中是一条曲线。
右上角的  并不是表示一个特定点的值,而是表示这条曲线是以
并不是表示一个特定点的值,而是表示这条曲线是以  为自变量、
为自变量、  为常量的函数图形。
为常量的函数图形。
当  时,函数值为
时,函数值为  ,如图中左上方所示。水平的那条虚线是函数值为
,如图中左上方所示。水平的那条虚线是函数值为  的基线,用于与其他函数值对比。
的基线,用于与其他函数值对比。
 那条线在
那条线在  下方(前面已经分析过了,因为
下方(前面已经分析过了,因为  ),
),  又在
又在  的下方(前面也已经分析过了),所以Armijo-Goldstein准则可能会把极小值点(可接受的区间)判断在区间bc内。显而易见,区间bc是有可能把极小值排除在外的(极小值在区间ed内)。
的下方(前面也已经分析过了),所以Armijo-Goldstein准则可能会把极小值点(可接受的区间)判断在区间bc内。显而易见,区间bc是有可能把极小值排除在外的(极小值在区间ed内)。
所以,为了解决这个问题,Wolfe-Powell准则应运而生。
文章来源:http://www.codelast.com/
【3】Wolfe-Powell准则
在某些书中,你会看到“Wolfe conditions”的说法,应该和Wolfe-Powell准则是一回事——可怜的Powell大神又被无情地忽略了...
Wolfe-Powell准则也有两个数学表达式,其中,第一个表达式与Armijo-Goldstein准则的第1个式子相同,第二个表达式为:
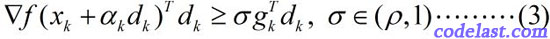
这个式子已经不是关于函数值的了,而是关于梯度的。
此式的几何解释为:可接受点处的切线斜率≥初始斜率的  倍。
倍。
上面的图已经标出了  那条线(即
那条线(即  点处的切线),而初始点(
点处的切线),而初始点(  的点)处的切线是比
的点)处的切线是比  点处的切线要“斜”的,由于
点处的切线要“斜”的,由于  ,使得
,使得  点处的切线变得“不那么斜”了——不知道这种极为通俗而不够严谨的说法,是否有助于你理解。
点处的切线变得“不那么斜”了——不知道这种极为通俗而不够严谨的说法,是否有助于你理解。
这样做的结果就是,我们将极小值包含在了可接受的区间内(  点右边的区间)。
点右边的区间)。
文章来源:http://www.codelast.com/
Wolfe-Powell准则到这里还没有结束!在某些书中,你会看到用另一个所谓的“更强的条件”来代替(3)式,即:
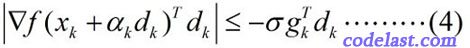
这个式子和(3)式相比,就是左边加了一个绝对值符号,右边换了一下正负号(因为  ,所以
,所以  )。
)。
这样做的结果就是:可接受的区间被限制在了 ![[b,d]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_af2fdeb93b85e5b0a49cb557cf999ebc.gif) 内,如图:
内,如图:
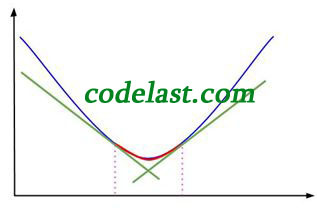
图中红线即为极小值被“夹击”的生动演示。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

博主写的非常好,用正常人能理解的语言解释的清楚
请问armij准则公式(2)按照泰勒展开证明的话,我怎么觉得和公式(1)一样都是左边<右边?
公式(1)乘以ρ∈(0,0.5),所以左边<右边;
公式(2)乘以(1-ρ)∈(0.5,1),所以左边也应该<右边吗?
楼主你太棒了,我最近也入坑优化啦,感谢楼主的解答~
感谢楼主,楼主好文章
请问能不能说一下规定ρ∈(0,1/2)的证明出处啊,我在袁亚湘写的《最优化理论与方法》没有找到Armijo的内容啊,是167页这个证明嘛
太久了,不记得具体位置了,隐约记得就是在那本书里
请问文中的g是函数f的梯度吗?因为wolfe-powell中又用哈密顿算子表示梯度,所以有点懵
是
g_k^T d_k <0 是d_k为下降方向的充要条件,这个结论能稍微解释一下吗,不太理解,多谢
可参考这个链接里的第【1】段:http://www.codelast.com/?p=7514
通俗易懂!不过看官们还要多看看相关代码加深理解。
个人之见:
看生涩之文可以俗语述之,可谓大神矣;
其后可以生涩入理之文述之,可谓小牛矣;
其后有人引述其生涩之文,可谓大牛矣!
回头又看了一遍这个文章,发现前面网友说的问题,“可接受的区间被限制在了[b,d]内,如图:”
感觉应该是[e,d]。不过不影响理解。
还有一个不好理解的地方,“Goldstein准则可能会把极小值点(可接受的区间)判断在区间bc内。显而易见,区间bc是有可能把极小值排除在外的(极小值在区间ed内)。所以,为了解决这个问题,Wolfe-Powell准则应运而生。”
个人补充一些不专业的分析以便理解:
Goldstein准则的第二条可能导致极值点被漏掉,那么需要寻找新搜索温和一些不至于漏掉极小点的alpha新搜索区间(横坐标)下界,以保证Goldstein准则第一条(因为要超线性收敛,这一条不能改)所确定的alpha新搜索区间上界有一个合理的下界,因此提出了Wolfe-Powell准则取代了Goldstein准则的第二条,二者结合在牺牲了一定效率的前提下,保证极小点不被漏掉。
个人理解,就是Goldstein准则的第一条负责大迈步缩小目标范围上界,Wolfe-Powell准则小步试探别把极小漏掉。
现在还没有很理解的就是:第一条的大步,为什么不会把极小值漏掉?我还要再理解理解。
再补充一点:我觉得Goldstein准则的第一条如果rho的值过大,也是有把极小值漏掉可能性的,之前自己调试仿真的时候,确实有完全找不到收敛点,曲线鬼画符一样的现象。
那么这样说下去,仿真时候,delta和rho的选取,就是rho尽量大(上界尽量小)和delta尽量适中,同时又不能漏掉极小值,以保证精确和效率之间的平衡。
delta的要适中是因为:斜率所对应的alpha值也就是下界。delta越小,下界减小的越快,对极小值的逼近越精确,书上说这样计算工作量大;delta越大,下界减小的越慢,对极小值的逼近越粗糙也就是弱,书上说这样计算工作量小。这需要在曲线上比划一下斜率的增减。
为什么delta越小,计算量越大,这个我还没有理解……继续理解理解……
我的理解是delta越小是离步长极值点的左边越远,delta大点的话,离极值点就会近点,那么搜索空间的左区间就会变小,那么就会使得迭代次数减少,从而减少。但是若是delta越过极值点的右侧的话,那么就可能使得避开了极值点。Wolfe-Powell准则就是精度和计算量的平衡了
想问一下 这个准则具体算法怎么做啊。怎么寻找ak。。
您好,请问如果是求矩阵的话,Armijo准则中,g'd 是一个矩阵不是一个数,怎么办啊。
请问您这个问题怎么解决的?
你的 rho 的范围(0,12)是不是有问题啊,谢谢
可接受点处的切线斜率≥初始斜率的倍
应该是小于吧,更平缓的点更好!
感谢,写的真好。
最后,“可接受的区间被限制在了[b,d]内,如图:”
是[e,d]吧?
写得很好,感谢分享!
http://web.mit.edu/6.252/www/LectureNotes/6_252%20Lecture04.pdf
顺手放一个描述Armijo-Goldstein的图..
楼主对我的帮助很大
楼主是不是在国科大读研一,我跟你感受差不多,很多大牛教材写的真的不适合初学者,到时老外的书写的图文并茂,通俗易懂,楼主写的很好,通俗易懂,很有共鸣,忘加油,谢谢!
不是读研,早工作了...
楼主是做啥工作的, 还会遇到这种问题