共轭方向法是介于最速下降法和牛顿法之间的一种存在——它的收敛速度(二阶收敛)比最速下降法(线性收敛)快,同时它的计算量又比牛顿法要小,因此它的存在是有意义的。
需要注意,共轭方向法可以不使用目标函数的一阶导数信息(当然也可以使用)。所以,如果目标函数的一阶导数不容易求的话,共轭方向法可能就可以派上用场了。
共轭方向法的显著特征就是:两次搜索方向之间是有关联的,这种关联就是“共轭”。
文章来源:http://www.codelast.com/
『1』向量共轭
先解释一下向量共轭的含义,你就明白共轭方向法的两次搜索方向之间的“共轭”是怎么回事了。
设  为对称正定矩阵,若
为对称正定矩阵,若  ,则称
,则称  和
和  为“G共轭”,共轭方向是“互不相关”的方向。
为“G共轭”,共轭方向是“互不相关”的方向。
『2』特性
当目标函数是二次函数  时,共轭方向法最多经过N步(N为向量维数)迭代,就可以到达极小值点——这种特性叫作二次收敛性(Quadratic Convergence)。
时,共轭方向法最多经过N步(N为向量维数)迭代,就可以到达极小值点——这种特性叫作二次收敛性(Quadratic Convergence)。
假设沿着一系列的共轭方向做迭代(寻找极小值点),这些共轭方向组成的集合叫作共轭方向集,则沿共轭方向集的每个方向顺序做line search的时候,在每个方向上都不需要做重复搜索——在任何一个方向上的移动,都不会影响到在另一个方向上已经找到的极小值。
上面这段描述是什么意思呢?我们先不讨论这些共轭方向是怎么计算出来的,拿一个在水平面上走路的例子来做比喻:你在水平方向A上走了10米,然后再沿着与水平方向垂直的另一个方向B上又走了10米,那么,你在方向A上走动的时候,在方向B上的坐标是不变的;你在方向B上走动的时候,在方向A上的坐标也是不变的。因此,把方向A和方向B看作两个共轭方向,那么,你在这两个共轭方向中的任何一个方向上移动,都不会影响到另一个方向上已经走到的坐标(把它想像成在这个方向上的极小值)。
文章来源:http://www.codelast.com/
但是世界哪有那么美好?目标函数不是二次函数的时候多得去了!这个时候,共轭方向法不就废了吗?非也非也。
理论与实践证明,将二次收敛算法用于非二次的目标函数,也有很好的效果。但是,这个时候,就不能保证N步迭代到达极小值点了。大家需要记住的是,很多函数都可以用二次函数很好地近似,这种近似在工程上是很重要。
有人一定会问,哪些函数可以用二次函数很好地近似呢?请原谅我没在书中看到这个总结,你只能自己去挖掘了。
『3』理论基础
共轭方向法有一个重要的理论基础,它是一个神奇的定理,有了它,可以推导出很多结论(共轭梯度法的理论推导就依赖于此)。
这里只把结论写上来,证明较长,不是本文关注的所以就不写了:
在精确line search的情况下,当前迭代点的梯度  与前面所有的搜索方向
与前面所有的搜索方向  直交:
直交:

这个结论在很多专业书中,都用了晦涩的描述来显示出教科书般的“高端、大气、上档次”,我看完之后只有一个感觉:看你们这些牛人写的书压力好大啊!
上面的红字,是我认为可以精简成“人话”之后的描述,也许它不严谨,也许它有漏洞,但是它大概说的就是这么回事,简单不就是美吗?
下面稍微解释一下定理中的一些概念:
 表明两个向量“直交”?从两个向量的夹角的数学定义:
表明两个向量“直交”?从两个向量的夹角的数学定义: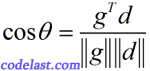
 为0时,整个式子为零,从而
为0时,整个式子为零,从而  ,也就是说两个向量的夹角是
,也就是说两个向量的夹角是  ,所以它们当然是“直交”的。
,所以它们当然是“直交”的。 这个式子中,当
这个式子中,当  的下标是
的下标是  时,
时,  的下标可以是
的下标可以是  ,例如,
,例如,  ,这表明,当前迭代点的梯度
,这表明,当前迭代点的梯度  与前面所有的搜索方向(
与前面所有的搜索方向(  )直交。
)直交。文章来源:http://www.codelast.com/
现在我把某书中一段和上面的理论等价的描述摘录下来,让大家看看它描述得是不是很晦涩:
共轭方向法在迭代过程中的每一个迭代点  都是目标函数
都是目标函数  在
在  和方向
和方向  所张成的线性流形
所张成的线性流形
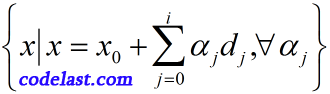
中的极小点。
 (此时
(此时  )是目标函数
)是目标函数  和方向
和方向  所张成的线性流形
所张成的线性流形  的极小值点。
的极小值点。 ,所以这就说明了
,所以这就说明了  是在
是在  方向上line search得到的极小值点,
方向上line search得到的极小值点,  是在
是在  方向上line search得到的极小值点。所以由基础定理可知,当前迭代点的梯度与前面所有方向的点积为零。
方向上line search得到的极小值点。所以由基础定理可知,当前迭代点的梯度与前面所有方向的点积为零。自己慢慢体会...
文章来源:http://www.codelast.com/
『4』基本流程
下面来看看,共轭方向法在迭代过程中是怎么做的。
假设迭代已经进行到了第  步,那么,下一步怎么走?
步,那么,下一步怎么走?
-
确定一个搜索方向要满足:
 ——这是为了满足目标函数值下降的条件(下降是最优化的目标),并且
——这是为了满足目标函数值下降的条件(下降是最优化的目标),并且  ——这是为了满足搜索方向之间的“共轭”条件。
——这是为了满足搜索方向之间的“共轭”条件。 -
检验迭代终止条件,若未终止,则用line search求
 ——在每一个搜索方向上,我们都要找到极小值点。
——在每一个搜索方向上,我们都要找到极小值点。 -
 ,继续迭代
,继续迭代
大家注意到,上面说确定一个搜索方向,要满足“共轭”的条件,问题是,共轭方向是如何获取的?光有愿望可不行啊。
文章来源:http://www.codelast.com/
『5』创造共轭方向
这里的关键是,如何构造出一个方向的集合,其N个方向线性无关、两两共轭?
有一个经典的方案就是Powell共轭方向集方法。
Powell是谁?
M.J.D. POWELL,剑桥大学教授(已故),世界著名的最优化专家。他是袁亚湘的导师(袁亚湘,中国科学院数学与系统科学研究院研究员、博士生导师,美国数学学会首届会士(2012年),中国科学院院士)。
Powell方法是一种不需要求目标函数导数的方法(zero-order method)。有一篇英文文章里说,如果你只需要知道一种zero-order method如何编程实现的话,那么一定是选Powell方法,可见Powell方法是有其重要地位的。
关于Powell方法,可以参考一下这篇文章,本文不详述。
文章来源:http://www.codelast.com/
『6』Powell方法的问题及改进
Powell方法产生的共轭方向集可能会变得线性相关,这会导致最终我们求得的,是N维空间的一个子空间内的极小值,而不是整体的极小值,所以,人们对Powell方法研究出了一些改进方案,例如:
- N轮迭代后,方向集重置为基向量;
- Brent(就是Brent's method的作者)提出,N轮迭代后,可以将方向集重置为任意正交矩阵(见下面的说明)的列向量;
- 放弃目标函数下降最大的方向,用一些好的方向代替N个必须共轭的方向;
- ...
PS:什么是正交矩阵?
一个实数正交矩阵是方块矩阵Q,它的转置矩阵是它的逆矩阵:  ,其中,
,其中,  为单位矩阵:
为单位矩阵:

文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

共轭梯度迭代中的N怎么证明比最速下降的少呢?
"所以由基础定理可知,当前迭代点的梯度与前面所有方向的点积为零"还是没有明白,求指点