在最优化领域，有几个你绝对不能忽略的关键词：拟牛顿、DFP、BFGS。名字很怪，但是非常著名。下面会依次地说明它们分别“是什么”，“有什么用” 以及 “怎么来的”。
但是在进入正文之前，还是要先提到一个概念上的区别，否则将影响大家的理解：其实DFP算法、BFGS算法都属于拟牛顿法，即，DFP、BFGS都分别是一种拟牛顿法。
先从拟牛顿法（Quasi-Newton）说起。这个怪怪的名词其实很形象：这是一种”模拟“的牛顿法。那么，它模拟了牛顿法的哪一部分呢？答：模拟的就是牛顿法中的搜索方向（可以叫作“牛顿方向”）的生成方式。
牛顿法是什么？本文是基于你已经知道牛顿法的原理的假设，如果你不清楚，那么可以看我这篇文章，里面非常简单而又清晰地描述了牛顿法的原理。
了解了牛顿法的原理，我们就知道了：在每一次要得到新的搜索方向的时候，都需要计算Hesse矩阵（二阶导数矩阵）。在自变量维数非常大的时候，这个计算工作是非常耗时的，因此，拟牛顿法的诞生就有意义了：它采用了一定的方法来构造与Hesse矩阵相似的正定矩阵，而这个构造方法计算量比牛顿法小。这就是对它“有什么用”的回答了。
（1）DFP算法
下面，就从DFP算法来看看“拟牛顿”是如何实现的（DFP算法是以Davidon、Fletcher、Powell三位牛人的名字的首字母命名的）。
前面说了，Hesse矩阵在拟牛顿法中是不计算的，拟牛顿法是构造与Hesse矩阵相似的正定矩阵，这个构造方法，使用了目标函数的梯度（一阶导数）信息和两个点的“位移”（Xk-Xk-1）来实现。有人会说，是不是用Hesse矩阵的近似矩阵来代替Hesse矩阵，会导致求解效果变差呢？事实上，效果反而通常会变好。有人又会问为什么？那么就简要地说一下——
由牛顿法的原理可知如下几个等式：
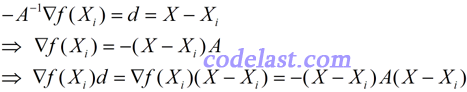
若最后一个等式子的最左边 < 0，即
，就是直观概念上的“沿方向d上，目标函数值下降”的表达。而在逐步寻找最优解的过程中，我们是要求目标函数值下降的，因此，应该有-(X-Xi)A(X-Xi) < 0，也即 (X-Xi)A(X-Xi) > 0。这表明矩阵A是正定的。而在远离极小值点处，Hesse矩阵一般不能保证正定，使得目标函数值不降反升。而拟牛顿法可以使目标函数值沿下降方向走下去，并且到了最后，在极小值点附近，可使构造出来的矩阵与Hesse矩阵“很像”了，这样，拟牛顿法也会具有牛顿法的二阶收敛性。
由于涉及到Hesse矩阵（二阶导数矩阵），我们当然要从目标函数 f(X) 的泰勒展开式说开去。与最优化理论中的很多问题一样，在这里，我们依然要假设目标函数可以用二次函数进行近似（实际上很多函数都可以用二次函数很好地近似）：
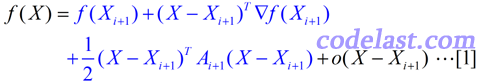
忽略高阶无穷小部分，只看前面的3项，其中A为目标函数的Hesse矩阵（二阶导数矩阵）。此式两边对X求导得：
于是，当 X=Xi 时，将[2]式两边均左乘(Ai+1)-1，有：
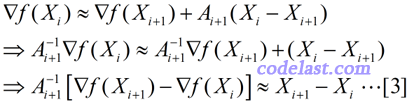
上式左右两边近似相等，但如果我们把它换成等号，并且用另一个矩阵H来代替上式中的A-1，则得到：
这个方程，就是拟牛顿方程，其中的矩阵H，就是Hesse矩阵的逆矩阵的一个近似矩阵。但是，从初始的H0开始，如何得到每一步迭代过程中需要的H1，H2，……呢？在迭代过程中生成的矩阵序列H0，H1，H2，……中，每一个矩阵Hi+1，都是由前一个矩阵Hi修正得到的，这个修正方法有很多种，这里只说DFP算法的修正方法。设：
然后又有问题：矩阵E怎么求？再设：
其中，m和n均为实数，v和w均为N维向量。将[6]代入[5]式，再将[5]式代入[4]式，可得：
[8]式与[7]式完全相同，只不过用简化的记号重写了一下。如果求出了m，n，v，w，就可以知道[6]式怎么求，从而进一步知道[5]式怎么求，从而我们的问题就彻底解决了。符合[7]这个方程的v，w可能有很多，但是我们有没有可能找到v，w的一个“特例”，使之符合这个等式呢？仔细观察一下，是可以找到的：[7]式的右边两个向量相减的结果，是一个n×1的向量，因此，等式左边的计算结果当然也是一个n×1的向量（每一项都是一个n×1的向量），所以我们把[7]式写成了[8]式的样子，可以看到，其中的第二、第三项中的括号里的向量的点积均为实数，这里，可以使第一个括号中的mvTqi值为1，使第二个括号中的nwTqi值为-1，这样的话，v只要取si，w只要取Hiqi，就可以使[8]式成立了。的确，这种带有一点猜测性质的做法，确实可以让我们找到一组适合的m，n，v，w值。
所以，我们得到的m，n，v，w值如下：
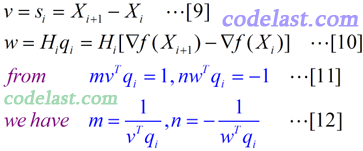
现在我们几乎大功告成了：将[8]~[11]代入[6]式，然后再将[6]代入[5]式，就得到了Hesse矩阵的逆矩阵的近似阵H的计算方法：
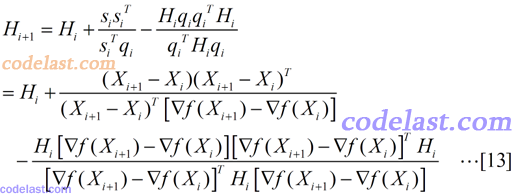
在上面的推导过程中，有人可能觉得有点无厘头：为什么[6]式要那样假设，是怎么想到的？我能给出的答案是：这一点我也没想明白。如果你知道，请告诉我，非常感谢。某些书上经常写类似于“很显然，XXX”之类的话，从一个定理直接得出了一个让人摸不着头脑的结论，而作为我这样比较笨的人来说，我觉得写书的很多专家们认为“很显然”的东西一点也不“显然”，甚至于有时候，我觉得那就像凤姐突然变成了范冰冰一样——一下子变出来了一个漂亮的结论，难以相信。所以这也是为什么我花费了很多时间，来把一些“很显然”的东西记下来，写明白的原因了。对于大多数牛人，他们需要的当然不是这种思维跨度这么小的文章，而是那种从地球可以一下子飞到火星的文章。所以，我写的东西不适合于水平高的人看，我只期望能帮助一小部分人就知足了。
说到这里，那么到底什么是DFP算法呢？上面的矩阵H的计算方法就是其核心，下面再用简单的几句话描述一下DFP算法的流程：
已知初始正定矩阵H0，从一个初始点开始（迭代），用式子 
来计算出下一个搜索方向，并在该方向上求出可使目标函数极小化的步长α，然后用这个步长，将当前点挪到下一个点上，并检测是否达到了程序中止的条件，如果没有达到，则用上面所说的[13]式的方法计算出下一个修正矩阵H，并计算下一个搜索方向……周而复始，直到达到程序中止条件。
有人会说，上面那些乱七八糟的都是搞什么啊，猜来猜去的就折腾出了一个公式，然后就确定这公式能用了？就不怕它在迭代的时候根本无法寻找到目标函数的极小值？正因为有这些疑问，所以在这里，还要提及一个非常重要的问题：我们通过带有猜测性质的做法，得到了矩阵H的计算公式，但是，这个修正过的矩阵，能否保持正定呢？前面已经说了，矩阵H正定是使目标函数值下降的条件，所以，它保持正定性很重要。可以证明，矩阵H保持正定的充分必要条件是：
并且，在迭代过程中，这个条件也是容易满足的。此结论的证明并不复杂，但是为了不影响本文的主旨，这里就没有必要写出来了。总之，我觉得作为一个最优化的学习者来说，首先要关注的是不是这些细节问题，而是先假设这些算法都适用，然后等积累到一定程度了，再去想“为什么能适用”的问题。
（2）BFGS算法
在上面的DFP算法的推导中，我们得到了矩阵H的计算公式，而BFGS算法和它有点像，但是比它形式上复杂一点。尽管它更复杂，但是在BFGS算法被Broyden，Fletcher，Goldfarb，Shanno四位牛人发明出来到现在的40多年时间里，它仍然被认为是最好的拟牛顿算法。历史总是这样，越往后推移，人们要超越某种技术所需的时间通常就越长。但是我们很幸运地可以站在巨人的肩膀上，从而可以在使用前人已经发明的东西的基础上感叹一声：这玩意太牛了。
好吧，又扯远了…… 回到中心主题，看看在BFGS算法中，与上面的[13]式一样的矩阵H是如何计算的：
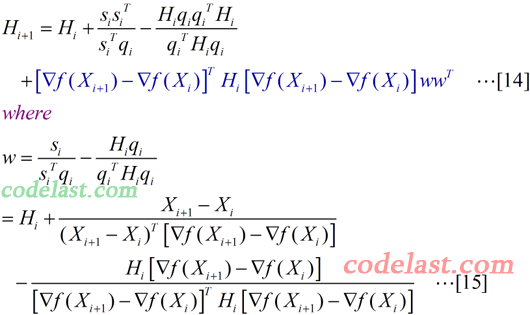
在[14]式中，最后一项（深蓝色的部分）就是BFGS比DFP多出来的东西。其中，w为一个n×1的向量。我们看到，由于向量w的表达式太长，所以没有把它直接写在[14]式中，而是单独列在了[15]式里。
可能[14]式一看就让人头晕，所以先来弱弱地解释一下这个式子的计算结果（如果你觉得好雷人，那么请直接无视）：wwT是一个n×1的向量与一个1×n的向量相乘，结果为一个n×n的矩阵，而[14]式中最后一项里，除了wwT之外的那一部分是（1×n）向量、n×n矩阵、n×1向量相乘，结果为一实数，因此[14]式最后一项结果为一个n×n矩阵，这与[14]式等号左边的矩阵H为n×n矩阵一致。这一点没有问题了。
在目标函数为二次型（“在数学中，二次型是一些变量上的二次齐次多项式”）时，无论是DFP还是BFGS——也就是说，无论[14]式中有没有最后一项——它们均可以使矩阵H在n步之内收敛于A-1。
延伸阅读：BFGS有一个变种（我不知道这样称呼是否正确），叫作“Limited-memory BFGS”，简称“L-BFGS”或“LM-BFGS”（这里的“LM”与Levenberg-Marquard算法没有关系），从它的名字上看，你肯定能猜到，使用L-BFGS算法来编写程序时，它会比BFGS算法占用的内存小。从前面的文章中，我们知道，BFGS在计算过程中要存储一个n×n的矩阵，当维数n很大的时候，这个内存占用量会很大——例如，在10万维的情况下，假设矩阵H中的元素以double来存储，那么，内存占用即为100000×100000×8÷1024÷1024÷1024≈74.5（GB），这太惊人了，一般的服务器几乎无法承受。所以，使用L-BFGS来降低内存使用量在某些情况下是非常有意义的。
关于L-BFGS的英文解释，请点击这个Wiki链接。由于我还没有深入学习L-BFGS，所以没办法在这里详细叙述了。
（全文完）
文章来源：https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处：codelast.com
感谢关注我的微信公众号（微信扫一扫）：
6式来自正交补空间和任意rank=1的方阵可分解为ata
用6公式是因为，人们希望每次迭代h能有一个微小的变化而不是巨大的变化，这样才有可能收敛。而公式6 这个变化是rank 1 的，是一种微小的变化，算是一种直觉➕常识吧。
修正一下，是rank 2
（13）的第二项分母应为delta_g的外积
我感觉博主的DFP 和 BFGS 说反了。 DFP 的 secant condition 即 公式4 是 H(x - x_k) = gradient x - gradient x_k 才对吧?
博主写的太赞了，豁然开朗，对于一些太基础的确实还不到细究的时候，大赞博主。期待新作。
公式13的第一个变换中有的最后一项有一个笔误，分子和分母中的Hi都缺少一个转置。
很好
公式6的设法，m,n为任意的常数，关键是E为一个对称矩阵，我们知道一个向量与自己的转职相乘就可以得到一个对称矩阵，所以这么设（这是我的猜测）
看了博主的文章才看懂《统计机器学习》的附录B(牛顿法和拟牛顿法)，谢谢！
BFGS的校正公式显得无头无脑，到底怎么出来的根本没提到，而直接把结果给出了。
按照书本上的介绍是按照DFP的形式定义Hessian矩阵逆，然后两次使用Sherman-Morrison公式
但我在这个地方碰到问题，书本上似乎“两次使用，就得到公式”这个过程是显然的，可我做不出，盼赐教~!
我也是看不明白那个“两次使用Sherman-Morrison公式”是怎么做的，曾经推导过，但是没做出来...
(15)右边的Hi似乎是多余的