N年前,当我还是一个在校学生的时候,有一次到工厂里实习,看到某系统上运行的一个软件中显示的一条条曲线,以及其下的一些参数值,我问旁边开发那款软件的老师:某某值是怎么求出来的?老师说,是对曲线求导算出来的。当时我就心想,一个人开发出这款软件得综合多少个领域的知识才能做得到啊。从那时起,我的心中就埋下了一颗种子。时光匆匆,一眨眼就到了今天,因为学习其他算法的原因,涉及到了一些求导算法的编程,于是,本文必须得写。
求导算法应用广泛,例如,在LM算法中,需要对函数求导(但是,使用数值求导的方法来求导数值,会不会对LM算法的整个过程的效率造成较大影响,我不清楚,还没有试验),可以考虑使用数值求导算法来实现。
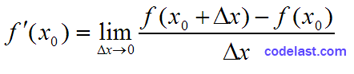
即:
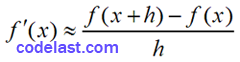 …………(A)
…………(A)
使用该式来求导时,由于在计算机内以二进制表示的数值不是一个精确值,而是一个有舍入误差的值,所以这样求出来的导数值,最多能精确到计算机精度的平方根——具体的推导过程这里就不写了。例如,你的计算机精度为10-12,则使用这种方法求导的精度只能达到10-6——即使你使用了一个10-12数量级的△x。可能你会觉得△x每减小一点,求出的导数就更精确一点,可惜,舍入误差会让你的期望落空。在很多场合下,这样大的计算误差是无法接受的。
我们现在考虑这样一种导数计算方法:
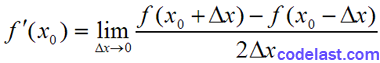
即:
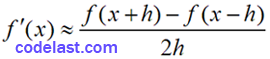 …………(B)
…………(B)
这个式子是怎么来的?由泰勒展式,可得:
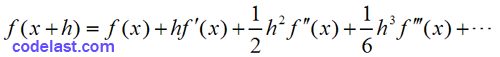
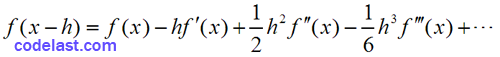
两式相减,得:
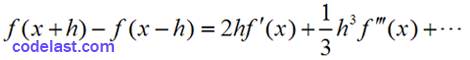
即:
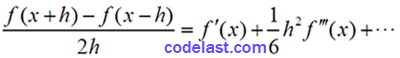
可见,用(B)式来求导时,截断误差为:

既然有了这个更胜一筹的求导式子,我们仅仅通过不断减小该式中的h的值来求导就行了吗?还是不行,因为我们仍然不知道一个合适的h是多大。
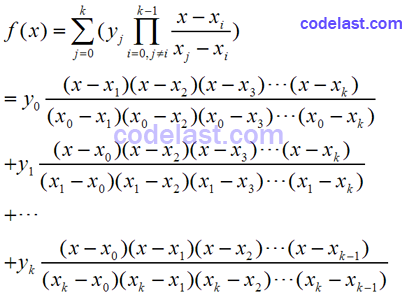
这个公式是干嘛的?它给出了经过(x0, y0),(x1, y1),……,(xk-1, yk-1) 这k个点的多项式插值公式。使用它,你可以计算出通过k个点的内插点或外推点的函数值(从函数形式上,我们可以很容易地验证出:f(x0)=y0,f(x1)=y1,……,f(xk-1)=yk-1,因此,拉格朗日插值函数必定是过这k个点的)。
知道了拉格朗日插值函数,那么它和Neville算法有何关系?使用拉格朗日插值公式来计算内插点很直观,但是,你无法知道这个计算结果的误差,并且用它不便于编程实现。而Neville算法使用了一种巧妙的、画出来像三角形的表来计算出拉格朗日插值函数的值,并且给出了误差的估计,而且还便于编程实现,所以,这也就是它存在的意义。
对应到Neville算法中,我们的插值函数就是上面的(B)式,自变量为h。由于h是未知的,甚至于初值都是猜测的,在寻找一个合适的h的过程中,我们需要构造出若干个已知的插值点(Neville表的第一列),然后再向Neville表的顶端推进,所以,与平常的插值在概念上有点“不太像”:在平常的插值过程中,我们会在若干已知的插值数据点所构成的区间范围内计算一个新点的纵坐标值,而这种情况更像是自变量h向“外”(超出已知范围的)推断猜测,所以我们称之为外推,而不是内插。
然后,我们的插值点如何构造呢?由于我们期待的逼近过程是h→0,因此,必然要创造出一系列越来越小的h,用它们来求出一系列的导数值(此即为Neville表的第1列,也就是相当于“已知”的点),然后再用外推的方法,求出Neville表的第2、3、……、最后一列。在这个过程中,待求的插值点的横坐标当然是h=0,如果你非要我说得明白一些的话,那就是:相当于Neville算法中的x为0。
至于“一系列越来越小的h”,我们可以通过指定一个初始的h值,并不断将其除以一个系数c(>1)的方式来得到。例如,x0=h,x1=h/c,x2=h/c2,……,xn=h/cn。横坐标为x=0的点没有包含在这些值所构成的区间的范围之内,这也就更说明了我们将这个逼近过程称为“外推”(而不是“内插”)的合理性。
为了更清楚地表示Neville表的结构,请看我画的这张图(以4阶的Neville表为例):

在向Neville表顶端推进的过程中,如果把上图中的每个P称为一个数据点的话,则:各数据点的计算可以按图中的箭头方向,以从上到下、从左到右的顺序逐项计算出来,这样的话,可以尽可能地减少计算函数值的次数,提高程序的效率。因为在逼近过程中,如果遇到了误差增大到一定程度的情况,求导过程就结束了,这样,下面的数据流就没有必要进行了(在这里,请允许我把x1→y1→P01这样的一个数据计算过程称作一个数据流)。
在Neville算法中,子结点的计算只依赖于两个父结点,因此,图中所示的数据计算流程是可以实现的,并且这种概念比原始意义上的Neville算法更好——原始意义上的Neville算法以“第1列→第2列→第3列→第4列”的顺序计算各项数据,因此无可避免地使第一轮计算过程中就对所有插值点的函数值进行计算,显然,这样做的效率不佳。所以说Ridders算法设计巧妙啊,这就是其优秀原因之一了。
上面就是Ridders求导算法的原理,我个人觉得,如果你原来已经略知一二的话,那么我这篇文章能为你增强一部分理解;但如果你一点也没听说过的话,只看此文并不能使你理解细节问题,你还是要去查很多很多的资料才行。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

一点小问题,Langrange 插值法连乘符号中,i的上限应该为k,与j相同。
好文章!
刚搜索到你的这篇帖子,我之前实现的一个自动求导的 C++ 库,就是用的这个算法。https://github.com/fengwang/derivative 欢迎赐教。