[原创] LM(Levenberg-Marquard)算法的实现

 

LM算法，全称为Levenberg-Marquard算法，它可用于解决非线性最小二乘问题，多用于曲线拟合等场合。

LM算法的实现并不算难，它的关键是用模型函数 $f$ 对待估参数向量 $p$ 在其邻域内做线性近似，忽略掉二阶以上的导数项，从而转化为线性最小二乘问题，它具有收敛速度快等优点。LM算法属于一种“信赖域法”——所谓的信赖域法，此处稍微解释一下：在最优化算法中，都是要求一个函数的极小值，每一步迭代中，都要求目标函数值是下降的，而信赖域法，顾名思义，就是从初始点开始，先假设一个可以信赖的最大位移 $s$ ，然后在以当前点为中心，以 $s$ 为半径的区域内，通过寻找目标函数的一个近似函数（二次的）的最优点，来求解得到真正的位移。在得到了位移之后，再计算目标函数值，如果其使目标函数值的下降满足了一定条件，那么就说明这个位移是可靠的，则继续按此规则迭代计算下去；如果其不能使目标函数值的下降满足一定的条件，则应减小信赖域的范围，再重新求解。

事实上，你从所有可以找到的资料里看到的LM算法的说明，都可以找到类似于“如果目标函数值增大，则调整某系数再继续求解；如果目标函数值减小，则调整某系数再继续求解”的迭代过程，这种过程与上面所说的信赖域法是非常相似的，所以说LM算法是一种信赖域法。

 

LM算法需要对每一个待估参数求偏导，所以，如果你的目标函数 $f$ 非常复杂，或者待估参数相当地多，那么可能不适合使用LM算法，而可以选择Powell算法——Powell算法不需要求导。

 

至于这个求导过程是如何实现的，我还不能给出建议，我使用过的方法是拿到函数的方程，然后手工计算出其偏导数方程，进而在函数中直接使用，这样做是最直接，求导误差也最小的方式。不过，在你不知道函数的形式之前，你当然就不能这样做了——例如，你提供给了用户在界面上输入数学函数式的机会，然后在程序中解析其输入的函数，再做后面的处理。在这种情况下，我猜是需要使用数值求导算法的，但我没有亲自试验过这样做的效率，因为一些优秀的求导算法——例如Ridders算法——在一次求导数值过程中，需要计算的函数值次数也会达到5次以上。这样的话，它当然要比手工求出导函数（只需计算一次，就可以得到导数值）效率要差得多了。不过，我个人估计（没有任何依据的，只是猜的）：依赖于LM算法的高效，就算添加了一个数值求导的“拖油瓶”，整个最优化过程下来，它仍然会优于Powell等方法。

文章来源：http://www.codelast.com/

在这篇解释信赖域算法的文章中，我们已经知道了LM算法的数学模型：

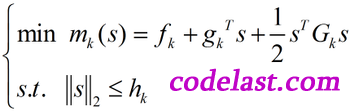
可以证明，此模型可以通过解方程组 $({G_k} + \mu I)s = - {g_k}$ 确定 ${s_k}$ 来表征。
即：LM算法要确定一个 $\mu \ge 0$ ，使得 ${G_k} + \mu I$ 正定，并解线性方程组 $({G_k} + \mu I){s_k} = - {g_k}$ 求出 ${s_k}$ 。
文章来源：http://www.codelast.com/
下面来看看LM算法的基本步骤：

• 从初始点 ${x_0}$ ， ${\mu _0} > 0$ 开始迭代
• 到第 $k$ 步时，计算 ${x_k}$ 和 ${\mu _k}$
• 分解矩阵 ${G_k} + {\mu _k}I$ ，若不正定，令 ${\mu _k} = 4{\mu _k}$ 并重复到正定为止
• 解线性方程组 $({G_k} + {\mu _k}I){s_k} = - {g_k}$ 求出 ${s_k}$ 并计算 ${r_k}$
• 若 ${r_k} < 0.25$ ，令 ${\mu _{k + 1}} = 4{\mu _k}$ ；若 ${r_k} > 0.75$ ，令 ${\mu _{k + 1}} = \frac{{{\mu _k}}}{2}$ ；若 $0.25 \le {r_k} \le 0.75$ ，令 ${\mu _{k + 1}} = {\mu _k}$
• 若 ${r_k} \le 0$ ，说明函数值是向着上升而非下降的趋势变化了（与最优化的目标相反），这说明这一步走错了，而且错得“离谱”，此时，不应该走到下一点，而应“原地踏步”，即 ${x_{k + 1}} = {x_k}$ ，并且和上面 ${r_k} < 0.25$ 的情况一样对 ${\mu _k}$ 进行处理。反之，在 ${r_k} > 0$ 的情况下，都可以走到下一点，即 ${x_{k + 1}} = {x_k} + {s_k}$
• 迭代的终止条件： $\left\| {{g_k}} \right\| < \varepsilon$ ，其中 $\varepsilon$ 是一个指定的小正数（大家可以想像一下二维平面上的寻优过程（函数图像类似于抛物线），当接近极小值点时，迭代点的梯度趋于0）

文章来源：http://www.codelast.com/
从上面的步骤可见，LM求解过程中需要用到求解线性方程组的算法，一般我们使用高斯约当消元法，因为它非常稳定——虽然它不是最快最好的算法。
同时，上面的算法步骤也包含对矩阵进行分解的子步骤。为什么要先分解矩阵，再解线性方程组？貌似是这样的（数学不好的人再次泪奔）：不分解矩阵使之正定，就无法确定那个线性方程组是有解的。矩阵分解有很多算法，例如LU分解等，这方面我没有看。

这里有一篇很不错的文章，解释了如何实现LM算法，大家可以参考一下。

需要说明的是，这是非线性无约束的问题，如果待估参数是有约束的（例如参数在某一范围内变动），要想用在LM算法中，那就是约束最优化问题了，这是一个big topic，以我目前的知识储备，尚不能解释好，请大家另寻资料吧。

文章来源：https://www.codelast.com/
➤➤ 版权声明 ➤➤ 
转载需注明出处：codelast.com 
感谢关注我的微信公众号（微信扫一扫）：