友情提示:如果觉得页面中的公式显示太小,可以放大页面查看(不会失真)。
Logistic Regression(或Logit Regression),即逻辑回归,简记为LR,是机器学习领域的一种极为常用的算法/方法/模型。
你能从网上搜到十万篇讲述Logistic Regression的文章,也不多我这一篇,但是,就像我写过的最优化系列文章一样,我仍然试图用“人话”来再解释一遍——可能不专业,但是容易看得懂。那些一上来就是几页数学公式什么的最讨厌了,不是吗?
所以这篇文章是写给完全没听说过Logistic Regression的人看的,我相信看完这篇文章,你差不多可以从无到有,把逻辑回归应用到实践中去。
Logistic Regression是一种分类算法。分类,也就是把一个群体(或问题,或数据)分为几个类别,例如,男/女/人妖;爱她的人/不爱她的人;今天会下雨/今天不会下雨。
Logistic Regression最常用于处理“二分类”问题,也就是说分类只有两个,像“爱她的人/不爱她的人”就是二分类,而“男/女/人妖”就不是二分类。当然,Logistic Regression也可以用于处理多分类问题,即所谓的“多分类逻辑回归”(Multiclass Logistic Regression),但本文并不涉及这个方面。
所以,说得简单点就是,给你一条数据,用Logistic Regression可以判断出这条数据应该被分到两个类别中的哪个中去。
文章来源:http://www.codelast.com/
Logistic Regression在现实世界中非常有用。例如,可以用它来判断一个用户是否会点击一个广告(会点击/不会点击),可以用Logistic Regression来判断两类人是否会相爱(会相爱/不会相爱),等等。
机器学习的主旨就是通过对历史数据的计算(即“学习”),得到一些未知参数的值,从而可以推断出新数据会有什么结论。例如一个非常简单的函数:  ,在已知几组
,在已知几组  历史数据的情况下:
历史数据的情况下:
(1, 5.5)
(1.5, 7)
(2, 6.5)
我们怎样能够预测一个未知的自变量  会对应什么样的因变量
会对应什么样的因变量  呢?也就是说,
呢?也就是说,  时
时 
显然我们的任务就是计算出两个未知参数  和
和  的值,有了这两个值,那么任意给定一个
的值,有了这两个值,那么任意给定一个  ,我们都能通过函数
,我们都能通过函数  计算出
计算出  的值了,这就是所谓的“预测”。
的值了,这就是所谓的“预测”。
文章来源:http://www.codelast.com/
Logistic Regression也是类似,我们有一个函数  ,里面包含若干个未知参数
,里面包含若干个未知参数  。
。
由于现实世界是复杂的,因变量  通常会跟很多因素(自变量
通常会跟很多因素(自变量  )有关系,即
)有关系,即  ,所以这里自变量是一个向量,这里用大写的
,所以这里自变量是一个向量,这里用大写的  来表示。同理,那一堆未知的参数也是一个向量,用一个字母
来表示。同理,那一堆未知的参数也是一个向量,用一个字母  来表示。
来表示。
现在给我们一堆  的历史数据,我们要想办法计算出所有未知参数的值,然后就可以拿来预测新的
的历史数据,我们要想办法计算出所有未知参数的值,然后就可以拿来预测新的  值所对应的
值所对应的  值了。
值了。
但是这个函数是什么呢?如下:
 ……(1)
……(1)
其中,  是参数向量,
是参数向量,  是自变量(向量)。
是自变量(向量)。
文章来源:http://www.codelast.com/
那么,这个略显奇怪的函数是怎么来的呢?
首先我们看  这部分:这是参数向量与自变量(向量)的点积,这个式子想要表达的含义是:计算某个事件发生的可能性,可以把跟这个事件相关的所有特征加权求和。例如,要求今天下雨的可能性,可以把今天所有和下雨相关的概率加权求和,例如梅雨季节权重为9(每天都很可能下雨),有台风经过权重为6,等等,每一个因素都影响着“下雨的可能性”,即:
这部分:这是参数向量与自变量(向量)的点积,这个式子想要表达的含义是:计算某个事件发生的可能性,可以把跟这个事件相关的所有特征加权求和。例如,要求今天下雨的可能性,可以把今天所有和下雨相关的概率加权求和,例如梅雨季节权重为9(每天都很可能下雨),有台风经过权重为6,等等,每一个因素都影响着“下雨的可能性”,即:

但是这个加权求和的结果是在  范围内的,为了能表示预测的概率,我们希望把输出值限制在
范围内的,为了能表示预测的概率,我们希望把输出值限制在  之间,而不是
之间,而不是  。所以,这时,逻辑函数就出场了。
。所以,这时,逻辑函数就出场了。
通过这个WiKi页面你可以知道,其实所谓的逻辑函数,就是这样的一个函数:

这个函数是由 Pierre François Verhulst(皮埃尔·弗朗索瓦·韦吕勒)在1844~1845年的时候给它起的名字。而我们上面的函数(1),就是这个形式。
逻辑函数的图像是这个样子的:
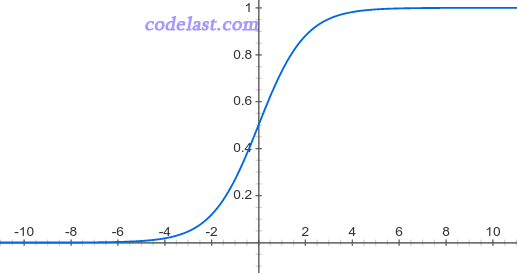
它的函数值刚好就是在(0,1)之间。
所以,我们通过逻辑函数,就可以计算出一个事件的概率了((0,1)之间)。但是不要忘了,我们前面说要处理二分类问题,得到一个(0,1)之间的任意值并不能归到两个分类中的一个里去,所以还要把这个概率值“归类”。其实这里很简单,我们可以在
 的时候,把它归到类别1中,
的时候,把它归到类别1中,  的时候,把它归到类别2中就可以了(概率值的“分水岭”可以根据实际情况调整)。用数学公式来表达这段话的含义就是:
的时候,把它归到类别2中就可以了(概率值的“分水岭”可以根据实际情况调整)。用数学公式来表达这段话的含义就是:

在各种机器学习的文章中,你都会看到,它们给了逻辑函数一个常用的名字:Sigmoid函数。sigmoid,意为“S形的”,这正符合其函数图像特点,所以大家记住就行了。
文章来源:http://www.codelast.com/
现在,我们已经有了函数,下一步任务就是求出函数表达式中的未知参数向量  了。这个过程是机器学习中最为核心的计算步骤。
了。这个过程是机器学习中最为核心的计算步骤。
以前面讲过的函数  为例:
为例:
你会发现,当已知几组  数据的情况下:
数据的情况下:
(1, 5.5)
(1.5, 7)
(2, 6.5)
你无论如何也不可能找到一对  和
和  的值,使得以上3组数据能精确地满足方程
的值,使得以上3组数据能精确地满足方程  ,正如下面的图像所示:
,正如下面的图像所示:
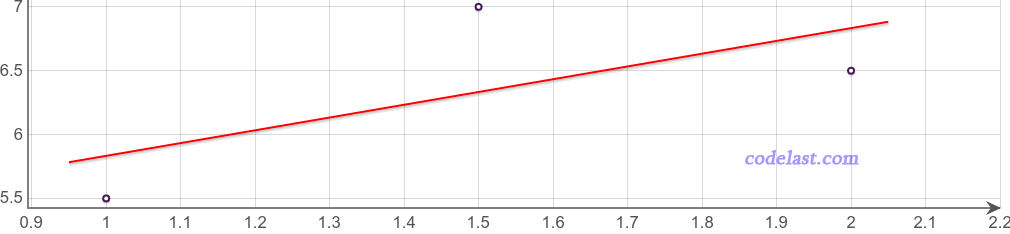
这条直线如果要精确地通过其中的两个点,那么就不能通过第三个点。所以,最终求出来的  和
和  的值,并不是方程的解析解,而是“最优解”。
的值,并不是方程的解析解,而是“最优解”。
因此,问题在于,我们如何画一条直线,使得其是“最优”的?“最优”的评判标准是什么?
文章来源:http://www.codelast.com/
为了理解“最优”,我们需要先了解一些概念。
- 损失函数/Loss Function/代价函数/Cost Function
按WiKi的定义:
In mathematical optimization, statistics, decision theory and machine learning, a loss function or cost function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function.
The loss function quantifies the amount by which the prediction deviates from the actual values.
文章来源:http://www.codelast.com/
所以现在问题来了,损失函数的表达式又是什么?
在探讨损失函数的表达式之前,我们先来看一下损失函数有哪些种类。
损失函数有很多种,例如下面几个:
(1)0-1损失函数:可用于分类问题,即该函数用于衡量分类错误的数量,但由于此损失函数是非凸(non-convex)的,因此在做最优化计算时,难以求解,所以,正因为如此,0-1损失函数不是那么“实用”(如果这句话有误,请指正)。
(2)平方损失函数(Square Loss):常用于线性回归(Linear Regression)。
(3)对数损失(Log Loss)函数:常用于其模型输出每一类概率的分类器(classifier),例如逻辑回归。
(4)Hinge损失函数:常用于SVM(Support Vector Machine,支持向量机,一种机器学习算法)。中文名叫“合页损失函数”,因为hinge有“合页”之意。这个翻译虽然直白,但是你会发现,99%的文章都不会用它的中文名来称呼它,而是用“Hinge损失”之类的说法。
这些都是人们的经验总结,当然,说每一种损失函数常用于什么机器学习算法,也都是有数学依据的。但是在这里,我们讲的是Logistic Regression,所以只看对数损失函数。对数损失函数通常用于衡量分类器(classifier)的精度,这里的“分类器”也就是指机器学习的模型,它对每一个类别输出一个概率值。从前面的文章中,我们已经知道了,逻辑回归就是这样一种分类器,所以才用对数损失函数来衡量其精度。
有时候,对数损失函数(Log Loss)也被叫作交叉熵损失函数(Cross-entropy Loss)。交叉熵这个名字比较拗口,在信息理论中,熵用于衡量某种事件的“不可预测性”,而交叉熵=事件的真实分布+不可预测性,所以交叉熵可以用于度量两个概率分布(真实分布&预测分布)之间的差异性,即:交叉熵损失函数(对数损失函数)可以衡量一个模型对真实值带来的额外噪音,通过最小化交叉熵损失函数(对数损失函数),我们就可以最大化分类器(模型)的精度。
上面这一大段话试图用简单的描述让你相信,为什么要用Log Loss来衡量Logistic Regression的误差,但是没有给出证明。有人可能会说,为什么不能用其他的方法来衡量,例如用平方损失函数(Square Loss)。事实上,这是有数学依据的——它会导致损失函数是一个关于参数向量  的非凸函数,而用对数损失函数就没有这种问题。凸函数的性质为我们后面求解参数向量
的非凸函数,而用对数损失函数就没有这种问题。凸函数的性质为我们后面求解参数向量  提供了极大便利,非凸函数有很多局部最优解,不利于求解
提供了极大便利,非凸函数有很多局部最优解,不利于求解  的计算过程。
的计算过程。
文章来源:http://www.codelast.com/
到这里为止,我们还是没有提到损失函数的数学表达式,但是如果要计算损失函数的值,我们是回避不了的,必须要知道。所以,这里用 L 来表示损失函数(取Loss之意),则对数损失函数的表达式为:
![L = - \frac{1}{n}\sum\limits_{i = 1}^n {[{y_i}\log ({{\hat y}_i}) + (1 - {y_i})\log (1 - {{\hat y}_i})]}](https://www.codelast.com/wp-content/plugins/latex/cache/tex_276a829ddba9850126edcea1af119036.gif) ......(2)
......(2)
其中,  是第i个真实值(
是第i个真实值(  ),
),  是第i个预测值。
是第i个预测值。
这个对数损失函数的表达式中并没有出现我们要求解的参数  ,所以我们把
,所以我们把  代到(2)式中去:
代到(2)式中去:
![L = - \frac{1}{N}\sum\limits_{i = 1}^n {\left[ {{y_i}\log \left( {\frac{1}{{1 + {e^{ - {\theta ^T}{X_i}}}}}} \right) + (1 - {y_i})\log \left( {1 - \frac{1}{{1 + {e^{ - {\theta ^T}{X_i}}}}}} \right)} \right]}](https://www.codelast.com/wp-content/plugins/latex/cache/tex_961181b6fd923c712b21a4cb9334697a.gif)
再来仔细看一下这个式子:N 为数据集的条数(有多少组  ,N就是多少),已知;
,N就是多少),已知;  是真实值,已知;
是真实值,已知;  是输入的向量,也已知。所以整个式子里只有
是输入的向量,也已知。所以整个式子里只有  是未知的,可以记为
是未知的,可以记为  ,称之为目标函数:
,称之为目标函数:
![L(\theta ) = - \frac{1}{N}\sum\limits_{i = 1}^n {\left[ {{y_i}\log \left( {\frac{1}{{1 + {e^{ - {\theta ^T}{X_i}}}}}} \right) + (1 - {y_i})\log \left( {1 - \frac{1}{{1 + {e^{ - {\theta ^T}{X_i}}}}}} \right)} \right]}](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ea3fb6a016e9c65dd4bae8aeb9ee1f68.gif)
因此,我们只要找到一个参数向量  ,能使得此式的值最小,那么这个参数向量
,能使得此式的值最小,那么这个参数向量  就是“最优”的参数向量。
就是“最优”的参数向量。
求得了这个最优的  之后,把它代入式(1),则对任一个未知的
之后,把它代入式(1),则对任一个未知的  ,我们都可以计算出
,我们都可以计算出  值,然后再根据一个阈值把它调整到 0 或 1,就得到了这个
值,然后再根据一个阈值把它调整到 0 或 1,就得到了这个  所属的分类,这样,我们就完成了一次“预测”的过程。
所属的分类,这样,我们就完成了一次“预测”的过程。
文章来源:http://www.codelast.com/
- 求解方法
 怎么求解?
怎么求解?在大的方向上,你可以选择不使用搜索方向的算法(例如信赖域算法),也可以选择众多使用搜索方向的算法(例如梯度下降法)。
在是否计算目标函数的导数这个方面,你可以使用不用求目标函数导数的算法(例如Powell共轭方向集方法),也可以使用要求目标函数导数的算法(例如梯度下降法)。由于某些目标函数形式特别复杂,计算其导数特别麻烦,所以在这种时候,不用计算导数的算法可能大有帮助。
事实上,在现在各种机器学习library百花齐放的今天,我们基本上不需要自己编写这些算法的具体实现,只需要调用它们即可。例如,通过Spark的Machine Learning Library (MLlib),我们可以直接使用Stochastic gradient descent (SGD),Limited-memory BFGS (L-BFGS)等实现。但是对这背后的原理有所了解,对工作学习是有帮助的。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

爱你 作者太棒了
上data anlysis时讲到logistic regression,实在是听不懂印度教授讲的内容,看此文胜读十年书,感谢。
Thank you for your extremely detailed explanation Darran! It helps me a lot.
太感谢了!
非常棒的讲解,让人豁然开朗
非常感谢博主,没有数学基础的小白终于搞懂了!
非常好 很感谢
博主讲的很清晰易懂啊 之前对对数损失函数和交叉熵有疑惑 现在懂了
Excellent 1!! 希望能看到更多机械学习的文章
收获太多,感谢作者分享
人話 讓人類更好理解
感謝作者!
感谢楼主!
万谢,解答了我的疑惑,博主加油哦
看了你的评论我对我来说就是醍醐灌顶 谢谢! 很想认识你
您寫得太好了, 讓我心領神會。有個問題想再請教一下,關於θ訓練出來之後帶入式子1, 是要用什麼門檻值來決定是屬於第1類還是屬於2類呢? 還是通常都使用0.5 呢?
这个阈值是根据业务的实际情况来设置/调整的,并不是个固定值,需要根据数据来分析。
你的答案就是我想要的
发现了一个干货博客,好玩的内容也很多,好开心,收藏之!
您写的非常好。