《Deep Learning》(Ian Goodfellow & Yoshua Bengio & Aaron Courville)第四章「数值计算」中,谈到了上溢出(overflow)和下溢出(underflow)对数值计算的影响,并以softmax函数和log softmax函数为例进行了讲解。这里我再详细地把它总结一下。
『1』什么是下溢出(underflow)和上溢出(overflow)
实数在计算机内用二进制表示,所以不是一个精确值,当数值过小的时候,被四舍五入为0,这就是下溢出。此时如果对这个数再做某些运算(例如除以它)就会出问题。
反之,当数值过大的时候,情况就变成了上溢出。
『2』softmax函数是什么
softmax函数如下:

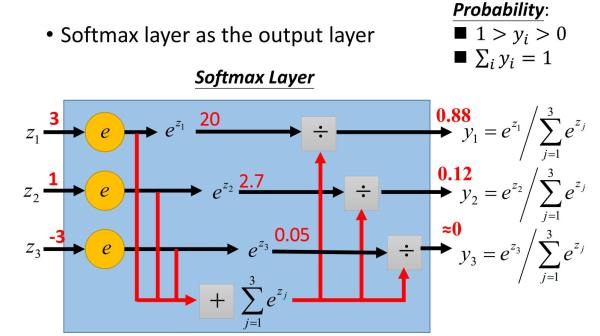
从公式上看含义不是特别清晰,所以借用知乎上的一幅图来说明(感谢原作者):
这幅图极其清晰地表明了softmax函数是什么,一图胜千言。
文章来源:https://www.codelast.com/
『2』计算softmax函数值的问题
通常情况下,计算softmax函数值不会出现什么问题,例如,当softmax函数表达式里的所有 xi 都是一个“一般大小”的数值 c 时——也就是上图中,  时,那么,计算出来的函数值
时,那么,计算出来的函数值  。
。
但是,当某些情况发生时,计算函数值就出问题了:
-
c 极其大,导致分子计算
 时上溢出
时上溢出 -
c 为负数,且
 很大,此时分母是一个极小的正数,有可能四舍五入为0,导致下溢出
很大,此时分母是一个极小的正数,有可能四舍五入为0,导致下溢出
文章来源:https://www.codelast.com/
『3』如何解决
所以怎样规避这些问题呢?我们可以用同一个方法一口气解决俩:
令  ,即 M 为所有
,即 M 为所有  中最大的值,那么我们只需要把计算
中最大的值,那么我们只需要把计算  的值,改为计算
的值,改为计算  的值,就可以解决上溢出、下溢出的问题了,并且,计算结果理论上仍然和
的值,就可以解决上溢出、下溢出的问题了,并且,计算结果理论上仍然和  保持一致。
保持一致。
文章来源:https://www.codelast.com/
举个实例:还是以前面的图为例,本来我们计算  ,是用“常规”方法来算的:
,是用“常规”方法来算的:

现在我们改成:

其中,  是
是  中的最大值。
中的最大值。
可见计算结果并未改变。
文章来源:https://www.codelast.com/
这是怎么做到的呢?通过简单的代数运算就可以参透其中的“秘密”:

通过这样的变换,对任何一个 xi,减去M之后,e 的指数的最大值为0,所以不会发生上溢出;同时,分母中也至少会包含一个值为1的项,所以分母也不会下溢出(四舍五入为0)。
所以这个技巧没什么高级的技术含量。
文章来源:https://www.codelast.com/
『4』延伸问题
看似已经结案了,但仍然有一个问题:如果softmax函数中的分子发生下溢出,也就是前面所说的 c 为负数,且  很大,此时分母是一个极小的正数,有可能四舍五入为0的情况,此时,如果我们把softmax函数的计算结果再拿去计算 log,即 log softmax,其实就相当于计算
很大,此时分母是一个极小的正数,有可能四舍五入为0的情况,此时,如果我们把softmax函数的计算结果再拿去计算 log,即 log softmax,其实就相当于计算  ,所以会得到
,所以会得到  ,但这实际上是错误的,因为它是由舍入误差造成的计算错误。
,但这实际上是错误的,因为它是由舍入误差造成的计算错误。
所以,有没有一个方法,可以把这个问题也解决掉呢?
答案还是采用和前面类似的策略来计算 log softmax 函数值:
![\log [f({x_i})] = \log \left( {\frac{{{e^{{x_i}}}}}{{{e^{{x_1}}} + {e^{{x_2}}} + \cdots {e^{{x_n}}}}}} \right) = \log \left( {\frac{{\frac{{{e^{{x_i}}}}}{{{e^M}}}}}{{\frac{{{e^{{x_1}}}}}{{{e^M}}} + \frac{{{e^{{x_2}}}}}{{{e^M}}} + \cdots \frac{{{e^{{x_n}}}}}{{{e^M}}}}}} \right) = \log \left( {\frac{{{e^{\left( {{x_i} - M} \right)}}}}{{\sum\limits_j^n {{e^{\left( {{x_j} - M} \right)}}} }}} \right) = \log \left( {{e^{\left( {{x_i} - M} \right)}}} \right) - \log \left( {\sum\limits_j^n {{e^{\left( {{x_j} - M} \right)}}} } \right) = \left( {{x_i} - M} \right) - \log \left( {\sum\limits_j^n {{e^{\left( {{x_j} - M} \right)}}} } \right)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_1ae2bb47902237d025410897d8644e12.gif)
大家看到,在最后的表达式中,会产生下溢出的因素已经被消除掉了——求和项中,至少有一项的值为1,这使得log后面的值不会下溢出,也就不会发生计算 log(0) 的悲剧。
在很多数值计算的library中,都采用了此类方法来保持数值稳定。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

您好!
您的网站可能不可能接受客座帖子?
谢谢
按照「3」中的叙述,假设一组数据:(1,2,3,4,M),其中M接近正无穷,按照公式,虽然M的分子解决了上溢出,但是1,2,3的分子就会下溢出了,这怎么解决?
非常有用,博主不错,加油
此时分子是一个极小的正数
看似已经结案了,但仍然有一个问题:如果softmax函数中的分子发生下溢出,也就是前面所说的 c 为负数,且 |c| 很大,此时分母是一个极小的正数。。。这句话中,应该是“此时分子是一个极小的正数”